A ball throuwn vertically upwards with a speed of 19.6ms−1 from the top of a tower returns to the earth in 6s. Find the height of the tower.
Here u=19.6ms−1
g=−9.8ms−2
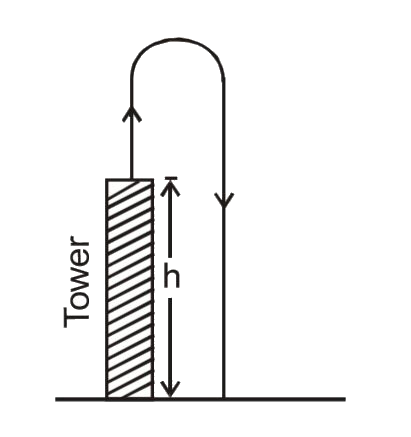
Net displacement, s = – h Negative sign is taken because displacement is in the opposite direction of initial velocity
As s=ut+12>2
∴ −h=19.6×6+12×(−9.8)×62
=117.6−176.4=−58.8
or h=58.8m
Topper's Solved these Questions
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 1 OBJECTIVE PROBLEMS
103 Videos
- KINEMATICSBOOK - MOTIONCHAPTER - KINEMATICSEXERCISE - EXERCISE 2 OBJECTIVE PROBLEMS
75 Videos
- HYDROSTATIC, FLUID MECHANICS & VISCOSITYBOOK - MOTIONCHAPTER - HYDROSTATIC, FLUID MECHANICS & VISCOSITYEXERCISE - EXERCISE -3 (SECTION-B) PREVIOUS YEAR PROBLEM
7 Videos
- KINETIC THEORY OF GASES BOOK - MOTIONCHAPTER - KINETIC THEORY OF GASES EXERCISE - EXERCISE-3 SECTION-B
16 Videos
Similar Questions
A ball throuwn vertically upwards with a speed of 19.6ms−1 from the top of a tower returns to the earth in 6s. Find the height of the tower.
View SolutionA ball thrown vertically upwards with a speed of 19.6ms−1 from the top of a tower returns to earth in 6s. Calculate the height of the tower.
View Solution
Knowledge Check
A ball throuwn vertically upwards with a speed of 19.6ms−1 from the top of a tower returns to the earth in 6s. Find the height of the tower.
A40 mB58.8 mC50 mD70 mA stone is thrown vertically upwards with an initial speed u from the top of a tower, reaches the ground with a speed 3u. The height of the tower is :
A3u2gB4u2gC6u2gD9u2gA ball is thrown vertically upwards with a speed of 10m/s from the top of a tower 200 m height and another is thrown vertically downwards with the same speed simultaneously. The time difference between them on reaching the ground is (g=10m/s2)
A12 sB6 sC2 sD1 s
A ball is thrown upwards with speed v from the top of a tower and it reaches the ground with speed 3v .The height of the tower is
View SolutionA ball is thrown upwards with speed ‘v’ from the top of a tower and it reaches the ground with a speed 3v, then the height of the tower is
View SolutionA particle is dropped from the top of a tower. It covers 40 m in last 2s. Find the height of the tower.
View SolutionA stone thrown upward with a speed u from the top of a tower reaches the ground with a velocity 4u. The height of the tower is
View SolutionA ball is projected vertically upwards with a velocity of 25ms−1 from the bottom of a tower. A boy who is standing at the top of a tower is unable to catch the ball when it passes him in the upward direction. But the ball again reaches him after 3 sec when it is falling. Now the boy catches it then the height of the tower is (g=10ms−2)
View Solution
