Question

Metal $M$ of radius $50nm$ is crystallized in $f$ type and made cubical crystal such that face of unit cells aligned with face of cubical crystal. If the total number of metal atoms of $M$ at all faces of cubical crystal is $6\times {10}^{30}$, then the area of one face of cubical crystal is $A\times {10}^{16}{m}^2$. Find the value of $A$.

Answer

2

Explanation

Consider one face of unit cell as shown below.

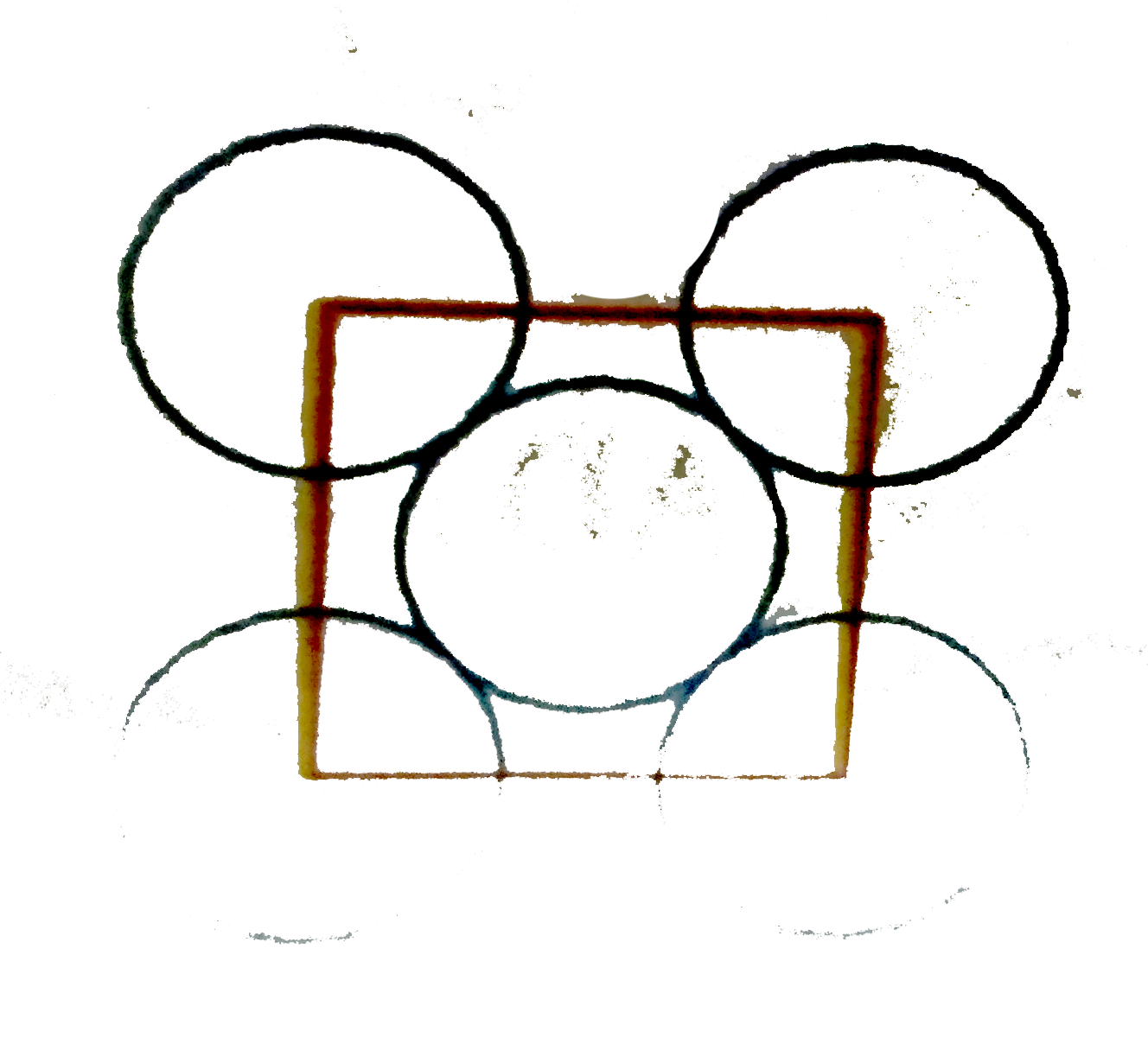
Number of atoms on one face=4(corners)
`xx(1)/(8)` (per corner share) +1 (face center) `xx(1)/(2)` (face center share)
`=(1)/(2)+(1)/(2)=1`/per face
Given number of atoms on all faces `=6xx10^(30)`
Given number of atoms on one face= `(1)/(6)xx6xx10^(30)=10^(30)` atoms.
Number of unit cells at one face of crystal= `(6xx10^(30))/(6)=10^(30)`
So, number of unit cells at the edge of crystal=`sqrt(10^(30))=10^(15)`
Now, edge length of unit cell `=(4)/sqrt(2)xx50`nm
Edge length of cubical crystal `=(4)/sqrt(2)xx50xx10^(15)nm`
So, area of face of crystal=`((4)/sqrt(2)xx50xx10^(15))^(@)nm^(2)`
`=(16)/(2)xx25xx10^(2)xx10^(30)=2xx10^(34)nm^(2)`
`=2xx10^(-18+34)m^(2)=2xx10^(16)m^(2)`
`therefore Axx10^(16)m^(2)=2xx10^(16)m^(2)rArrA=2`.