A hexagonal close-packed lattic can be represented by figures (a) and (b) below. If c=a√83=1.633a , there is an atom at each corner of the unit cell and another atom which can be located by moving one-third the distance along the diagonal of the rhombus base, starting at the lower left hand corner and moving perpendicularly upward by c/2 . Mg crystallizes in this lattice and has a density of 1.74gcm−3.
What is the volume of unit cell?
A
46
B
20
C
180
D
90
Video Solution
Text Solution
The correct Answer is:A
Zeff=8 (corners)×18 (per corner share)+1 (in the body)=2 atoms/unit cell.
Aw of Mg=24.3g
Mass=(2 atoms)
(24.3g6.02×1023atoms)=8.07×10−23g
volume=
MassDensity=(8.07×10−23g1.74gcm−3)×(108∘A)3=46.4∘A3
|
Similar Questions
Knowledge Check
A hexagonal close-packed lattic can be represented by figures (a) and (b) below. If c=a√83=1.633a , there is an atom at each corner of the unit cell and another atom which can be located by moving one-third the distance along the diagonal of the rhombus base, starting at the lower left hand corner and moving perpendicularly upward by c/2 . Mg crystallizes in this lattice and has a density of 1.74gcm−3.
What is the distance between nearest heighbours?
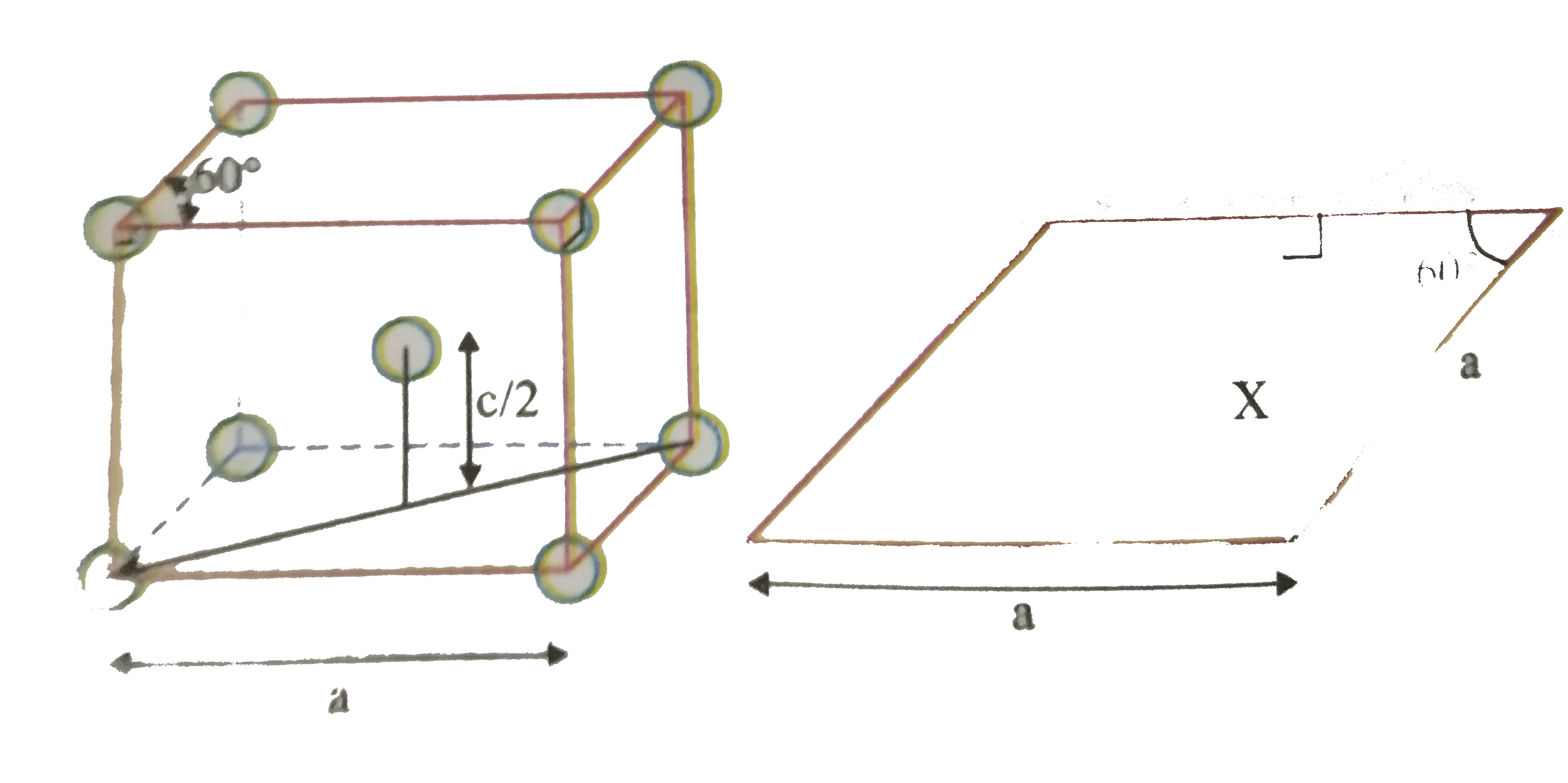 A1.6B3.2C4.6D8
A1.6B3.2C4.6D8Hexagonal close packing is found in crystal lattice of
ANaBMgCAlDNone of theseHexagonal close packing is found in crystal lattice of :
ANaBMgCAlDNone of these
Calculate the number of atoms in a cubic-shared unit cell having one atom on each corner and two atoms one each diagonal.
View SolutionHow many atoms are present in a cubic unit cell having one atom at each corner and two atoms on each body diagonal ?
View SolutionNumber of atoms per unit cell, if atoms are present at the corner of unit cell and 2 atoms at each body diagonal
View SolutionThe number of atoms in a cubic based unit cell having one atom on each corner and two atoms on each body diagonal is
View SolutionIn a face centred cubic arrangement of A and B atoms, A atoms are at the corners of the unit cell and B atoms at theface centres. One of the A atom is missing from one corner in the unit cell. The simplest formula of the compound is
View Solution