A compound made of particles A, B, and C forms ccp lattice. Ions A are

A compound made of particles $A$ , $B$ , and $C$ forms $p$ lattice. In the lattice, ions $A$ occupy the lattice points and ions $B$ and $C$ occuphy the alternate $T V_{s}$ . If all the ions along one of the body diagonals are removed, then formula of the compound is
A $A_{3.75} B_{3} C_{3}$
B $A_{3.75} B_{3} C_{4}$
C $A_{3} B_{3.75} C_{3}$
D $A_{3} B_{3} C_{3.75}$
A compound made of particles $A$ and $B$ . A forms $f c c$ packing and $B$ occupies all the $O V_{s}$ . If all the particles along the plane as shown in the figure below are removeed, then the simplest formula of the compound is

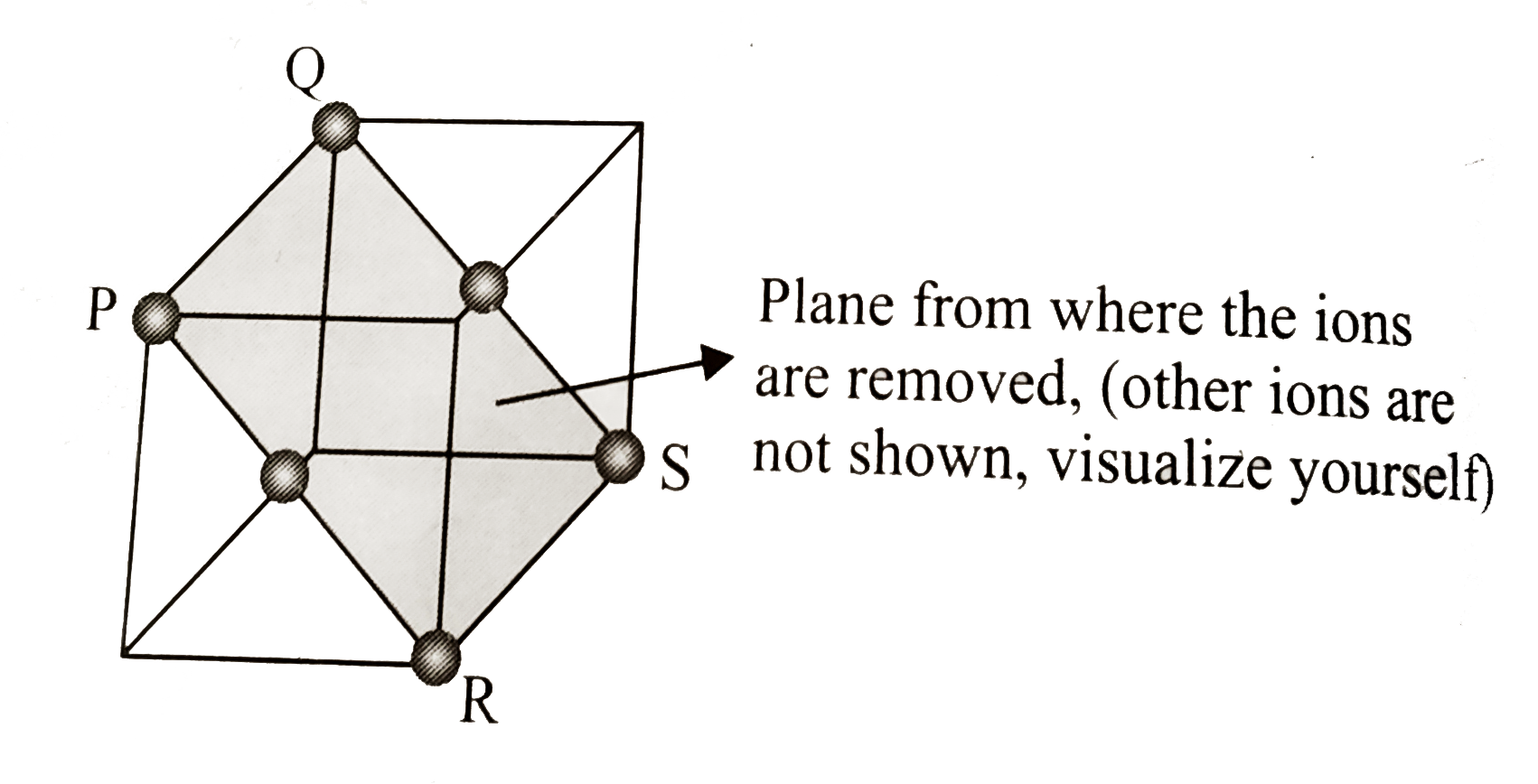A $A_{5} B_{7}$
B $A_{7} B_{5}$
C $A B$
D $A B_{3.75}$
A crystal is made of particles A and B. A forms FCC packing and B occupies all the octahedral voids. If all the particles along the plane as shown in figure are removed, then the formula of the crystal would be :
A $A_{5} B_{7}$
B $A_{7} B_{5}$
C $A B$
D $A B_{3.75}$

A compound made of particles $A$ , $B$ , and $C$ forms $p$ lattice. Ions $A$ are at lattice points, $B$ occupy $T V_{s} C$ occupy $O V_{s}$ . If all the ions along one of the edge axis are removed, then formula of the compound is