Assuming that in case of motion of blunt bodies in air acrodynamic drag depends on effective area a of the body, the speed of body relative to air v and density of air , show by method of dimensions:
Dimensions of 'D' that of force
Dimension of
Dimension of
Dimension of
k is dimensions less
Let,
from LHS and RHS
So, and
Topper's Solved these Questions
- UNITS AND DIMENSIONSBook:GRB PUBLICATIONChapter:UNITS AND DIMENSIONSExercise:Objective Type Question
Explore 103 Videos
- UNITS AND DIMENSIONSBook:GRB PUBLICATIONChapter:UNITS AND DIMENSIONSExercise:More than one choice is correct
Explore 17 Videos
- UNITS AND DIMENSIONSBook:GRB PUBLICATIONChapter:UNITS AND DIMENSIONSExercise:Link Compression
Explore 6 Videos
- MOTION IN TWO AND THREE DIMENSIONSBook:GRB PUBLICATIONChapter:MOTION IN TWO AND THREE DIMENSIONSExercise:All Questions
Explore 210 Videos
- VECTORSBook:GRB PUBLICATIONChapter:VECTORSExercise:PASSAGE -3
Explore 3 Videos
Similar Questions
The buoyant force F acting on a body depends on the density of medium ρ, volume of body immerese V and acceleration due to gravity g. Establish the relation using method of dimensions.
View SolutionA body dropped from a height H reaches the ground with a speed of 1.2 √gH. Calculate the work done by air friction.
View Solution
Knowledge Check
If W be the weight of a body of density ρ in vacuum then its apparent weight in air of density σ is
AWρσBW(ρσ−1)CWρσDW(1−σρ)A body of density d is conuterpoised by Mg of weights of density d1 in air of density d. Then the true mass of the body is
AMBM(1−d2)CM(1−dd1)DM(1−d/d2)(1−d/d1)A body weights x g in air, y g in liquid and z g in the water . The ratio of relative density of liquid and the body is
Ax−y:xBx−y:zCy−z:xDz−y:y
A body weight 20 N in water and its relative density is 3. Find the weight of the body in air.
View SolutionA pitot tube Fig. is used to determine the air speed of an airplane. It consists of an outer tube with a number of small holes B (four are shown that allow air into the tube, that tube is connected to one arm of a U-tube. The other arm of the U-tube is connected to hole A at the front end of the device, which points in the direction the plane is headed. At A the air becomes stagnant so that vA = 0. At B, however, the speed of the air presumably equals the airspeed v of the plane. (a) Use Bernoulli's equation to show that
v=√2ρghρair
where ρ is the density of the liquid in the U-tube and his the difference in the liquid levels in that tube. (b) Suppose that the tube contains alcohol and the level difference h is 20.0 cm. What is the plane's speed relative to the air? The density of the air is 1.03kg/m3 and that of alcohol is 810 kg/m3
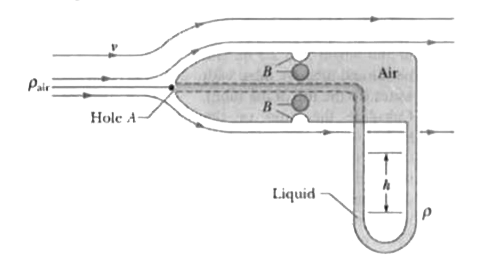
View SolutionA body weight 20 N in water and its relative density is 3. Find the weight of the body in air.
View SolutionAn electric fan, with effective area of cross-section 'A', accelerates air of density 'rho' to a speed 'v'. What is the power needed for this process ?
View SolutionWhen a body falls in a air, the resistance of air depends to a great extent on the shape of the body. The different shapes are givne. Identify the combination of air resistance which truly represents the physical situation?
(The cross-sectional areas are the same)
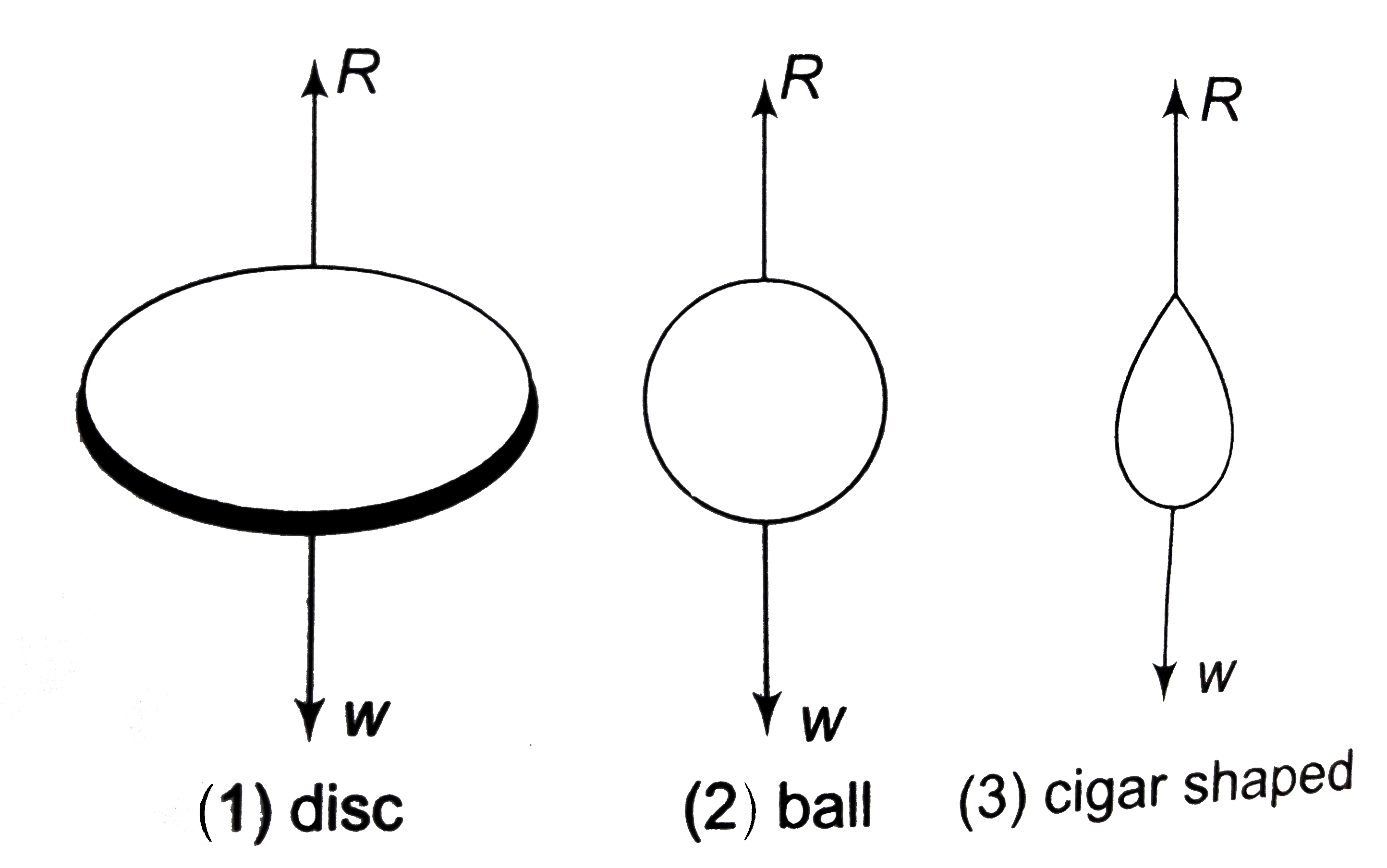
View Solution