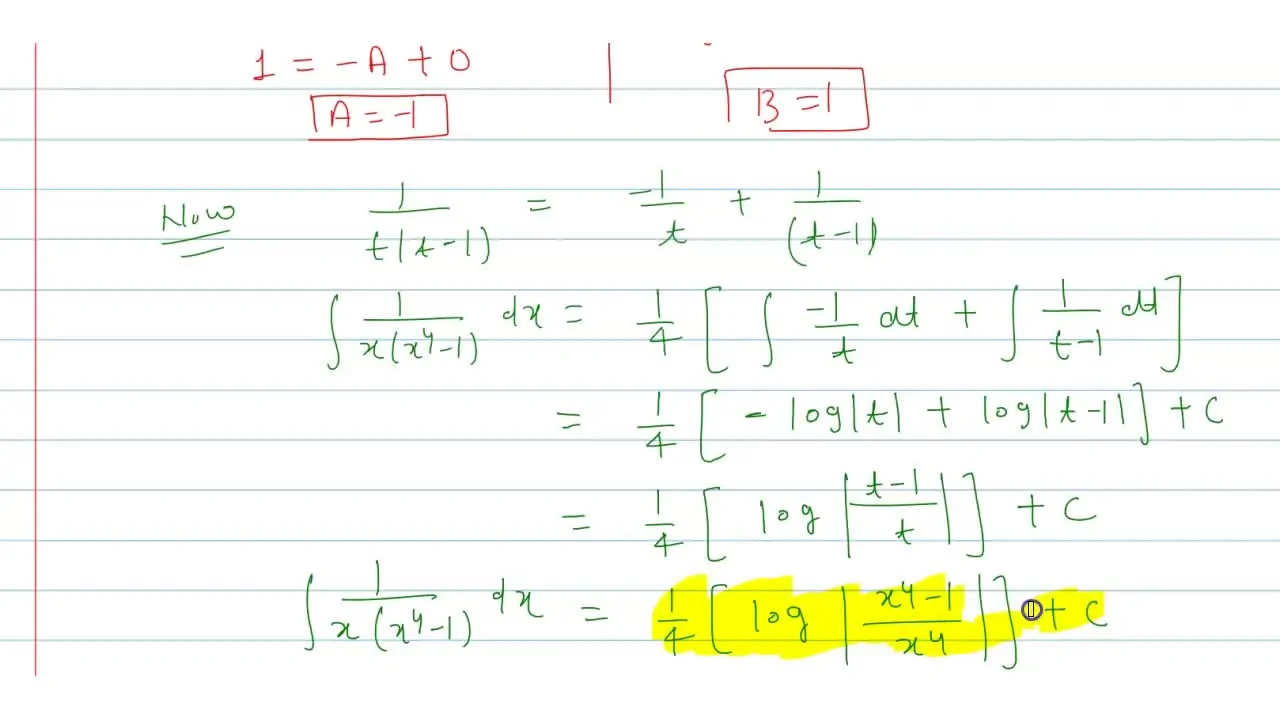Integrate the rational functions1x(x4−1)
Video Solution
Text Solution
Given 1x(x4−1)
Multiplying numerator and denominator by x3, we obtain
1x(x4−1)=x3x4(x4−1)
∴∫(1x(x4−1))dx=∫(x3x4(x4−1))dx
Let x4=t
⇒4x3dx=dt
⇒14∫(dtt(t−1))
Let 1t(t−1)=At+Bt−1
⇒1=A(t−1)+Bt..........(1)
Substituting t=0 and t=1 in eq(1) we obtain A=−1 and B=1
⇒1t(t−1)=−1t+1t−1
⇒14∫(−1t+1t−1)dt
=14(−logt+log(t−1)+c)
=14log(t−1t)+c
=14log(x4−1x4)+c
|
Updated on:21/07/2023
Related Playlists
- BOOK - NCERTCHAPTER - INTEGRALSEXERCISE - MISCELLANEOUS EXERCISE44videos
INTEGRALS
- BOOK - NCERTCHAPTER - INTEGRALSEXERCISE - EXERCISE 7.324videos
INTEGRALS
- BOOK - NCERTCHAPTER - INTEGRALSEXERCISE - EXERCISE 7.714videos
INTEGRALS
- BOOK - NCERTCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - EXERCISE 9.112videos
DIFFERENTIAL EQUATIONS
- BOOK - NCERTCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE17videos
INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
Integrate the rational functions1x4−1
View SolutionIntegrate the rational functions3x−1(x−1)(x−2)(x−3)
View SolutionIntegrate the rational functions1x(xn+1)[Hint: multiply numerator and denominator by xn−1and put xn=t]
View SolutionIntegrate the rational functionsx(x−1)(x−2)(x−3)
View SolutionIntegrate the rational functions1x2−9
View SolutionIntegrate the rational functionsx(x−1)2(x+2)
View SolutionIntegrate the rational functions1(ex−1)[Hint : Put ex=t]
View SolutionIntegrate the rational functions5x(x+1)(x2−4)
View SolutionIntegrate the rational functionsx3+x+1x2−1
View SolutionIntegrate the rational functionsx(x2+1)(x−1)
View Solution