A man is moving away from a tower 41.6 m high at the rate of 2 m/sec. Find the rate at which the angle of elevation of the top of tower is changing, when he is at a distance of 30m from the foot of the tower. Assume that the eye level of the man is 1.6m from the ground.
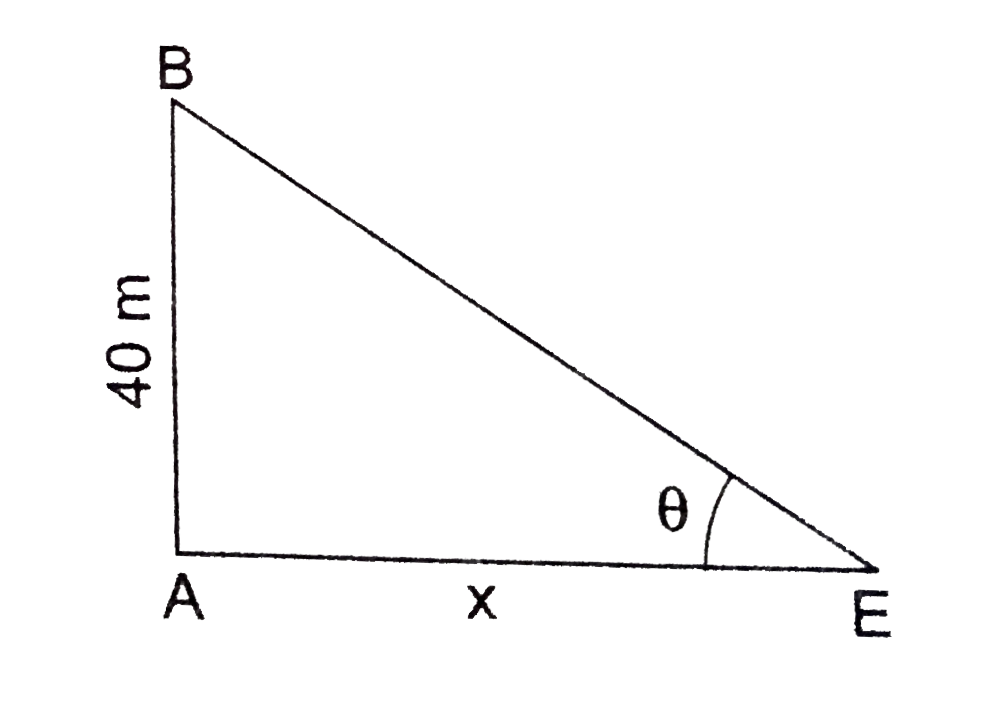
tanθ=BCPC=40x
x=40cotθ
dxdt=−40cosec2θdθdt
dxdt=2m∣sec
dθdt=−120cosec2θ
Whenx=30
cothθ=3040=34
cose^2θ=1+cot2θ
=1+416=2516
cosec2θ=2516
dthηdt=−4125 rad/sec.
Topper's Solved these Questions
Similar Questions
A man is moving away from a tower 41.6 m high at the rate of 2 m/sec. Find the rate at which the angle of elevation of the top of tower is changing, when he is at a distance of 30m from the foot of the tower. Assume that the eye level of the man is 1.6m from the ground.
View SolutionA man is moving away from a 40-m high tower at a speed of 2 m/s. Find the rate at which the angle of elevation of the top of the tower is changing when he is at a distance of 30 metres from the foot of the tower. Assume that the eye level of the man is 1.6 m from the ground.
View Solution
Knowledge Check
A man is moving away from a tower 41.6m high at a rate of 2ms−1. If the eye level of the man is 1.6m above the ground, then the rate at which the angle of elevation of the top of the tower changes, when he is at a distance of 30 m from the foot of the tower, is:
A−4125 radian/sB225 radian/sC−1625 radian/sDNone of theseThe angle of elevation of the top of a tower of height 100√3m from a point at a distance of 100 m from the foot of the tower on a horizontal plane is
A60∘B90∘C120∘D180∘The angle of elevation of the top of a tower of height 100√3m from a point at a distance of 100 m from the foot of the tower on a horizontal plane is
A60∘B90∘C120∘D180∘
The angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of the tower is 30∘. Find the height of the tower.
View SolutionFind the angle of elevation of a point which is at a distance of 30 m from the base of a tower 10√3 m high.
View SolutionWhat is the angle of elevation of the top of a tower from a point on the ground, which is 30 m away from the foot of a tower of height 10√3m?
View SolutionThe angle of elevation of the top of a tower at a point on the ground 20 m from the foot of the tower is 30∘. What is the height of the tower?
View SolutionThe angle of elevation of the top of a tower from a point on the ground, which is 30m away from the foot of the tower, is 30∘. Find the height of the tower.
View Solution
