Kinetic energy of a particle moving along elliptical trajectory is giv

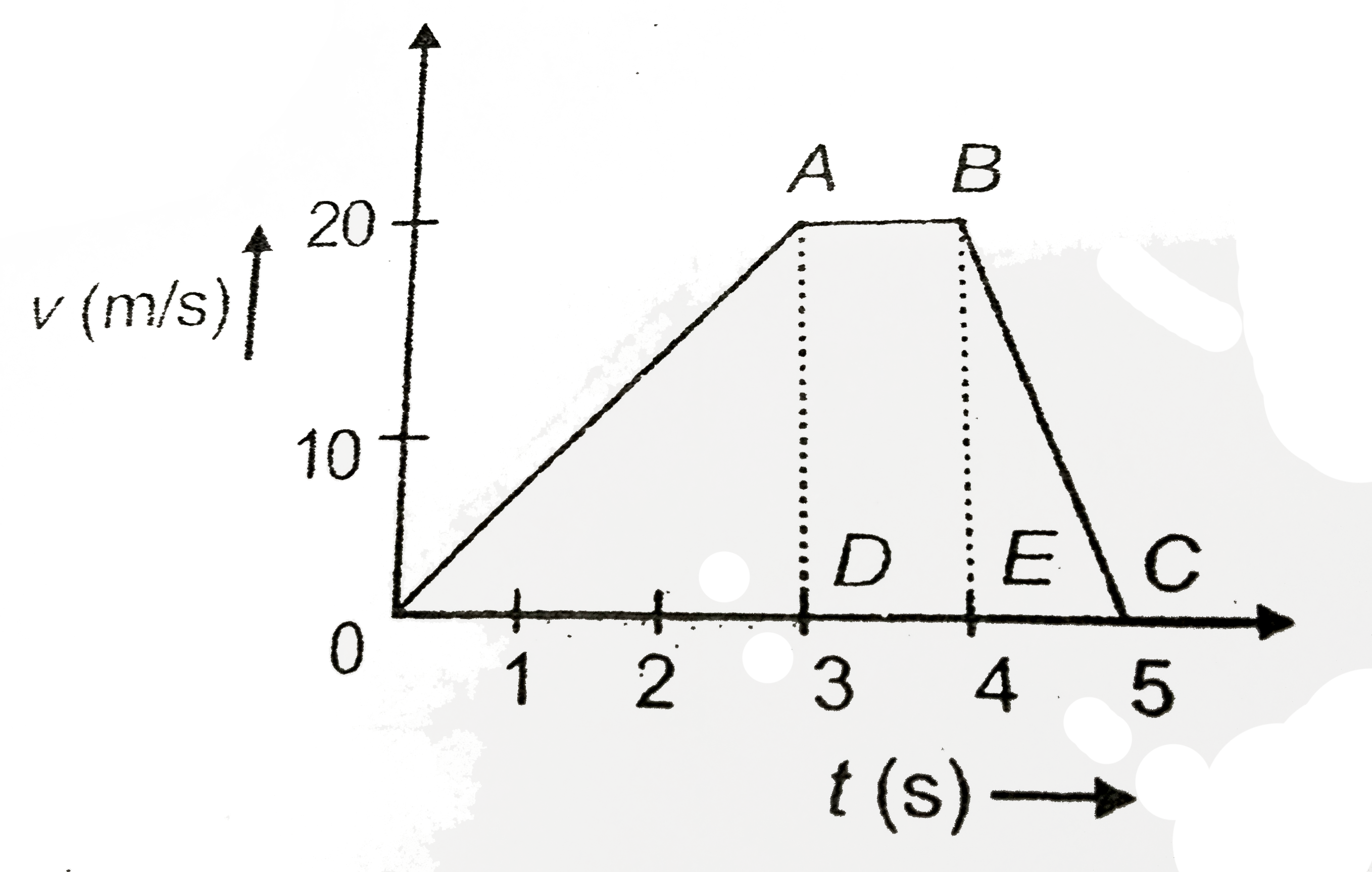
The variation of velocity of a particle moving along straight line is shown in the figure. The distance travelled by the particle in 4 s is

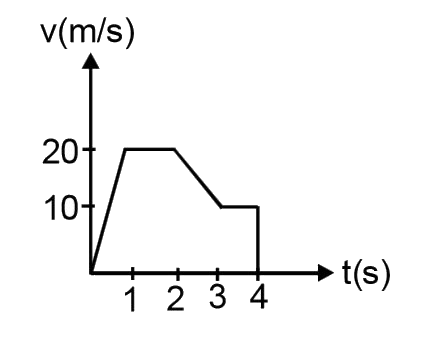A25m
B30m
C55m
D60m
The kinetic energy K of a particle moving along a circle of radius R depends upon the distance s as $K = a s^{2}$ . The force acting on the particle is
A(a) $2 a \frac{s^{2}}{R}$
B(b) $2 a s {[1 + \frac{s^{2}}{R}]}^{1 / 2}$
C(c) $2 a s$
D(d) $2 a$
Kinetic energy of a particle moving along a circle of radisu R depends on the distance covered as $K = a s^{2}$ where a is a constant . Find the force acting on the particle as a function of s.
A $\frac{2 a}{s} \sqrt{1 + {(\frac{s}{R})}^{2}}$
B $2 a s \sqrt{1 + {(\frac{R}{s})}^{2}}$
C $2 a s \sqrt{1 + {(\frac{s}{R})}^{2}}$
D $\frac{2 s}{a} \sqrt{1 + {(\frac{R}{s})}^{2}}$

Kinetic energy of a particle moving along elliptical trajectory is given by $K = α s^{2}$ where s is the distance travelled by the particle. Determine dimensions of $α$