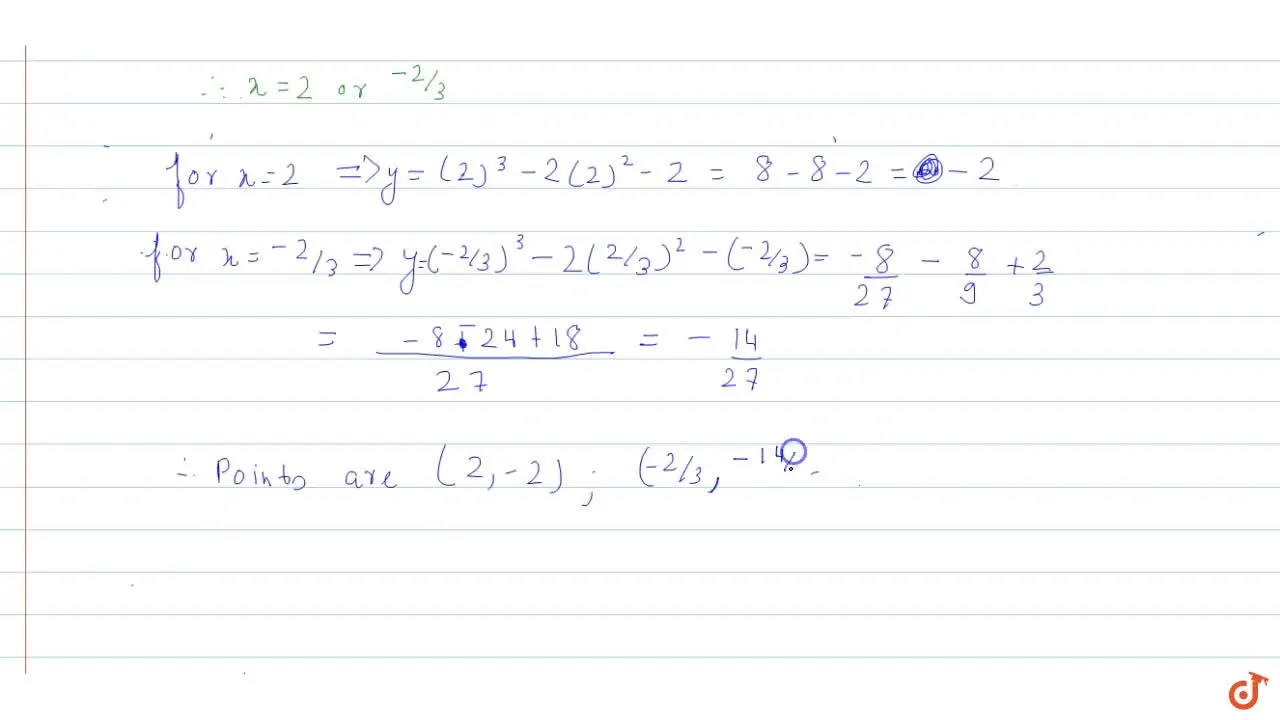Find the points on the curve y=x3−2x2−x at which the tangent lines are parallel to the line y=3x−2
y=mx+c,slope of this line=m
∴y=3x−2, slope of line y=3x−2is 3
slope of tangent of any curve is dydx at that point
y=x3−2x2−x
dydx=ddx(x3−2x2−x)
=3x2−4x−1
∴dydx=3
⇒3x2−4x−1=3
⇒3x2+2x−6x−4=0
∴x(3x+2)−2(3x+2)⇒(x−2)(3x+2)=0
∴x=2or−23
for x=2⇒y=(2)3−2(2)2−2=8−8−2=−2
for x=-2/3 ⇒y=(−23)3−2(23)2−(−23)
=−827−89+23
=−8+24+1827=−1427
∴ points are (2,−2);(−23.−1427)
Answer
Related Playlists
Similar Questions
Find the points on the curve x3−2x2−2x at which the tangent lines are parallel to the line y=2x−3 .
View SolutionFind the point on the curve y=3x2−4x+5 where the tangent line is parallel to the line y=-22x+7
View SolutionFind the points on the curve y=x3−2x2−x, where the tangents are parallel to 3x−y+1=0
View SolutionFind a point on the curve y=3x2−2x−4 at which the tangent is parallel to the line 10x−y+7=0.
View SolutionFind the points on the curve x2+y2−2x−3=0at which the tangents are parallel to the x-axis.
View SolutionFind the points on the curve y=x3−2x2+x at which the tangents are parallel to x-axis. Also find the tangents at these points.
View SolutionDetermine the points on the curve 2y=(3−x2) at which the tangent is parallel to the line x+y=0
View SolutionFind the point on the curve y=x3−x2−x+3, where the tangent is parallel to x-axis .
View SolutionFind the points on the curve x2+y2−2x−3=0 at which the tangents are parallel to the x-axis and y-axis.
View SolutionFind the points on the curve 2a2y=x3−3ax2 where the tangent is parallel to x-axis.
View Solution