Doubtnut Promotions Sticky

The curve y=0.005x2−2x+200 for 0≤x≤200 and the line segment from F(0.200) to G(200,0) are shown in the standard (x,y) coordinate plane below.
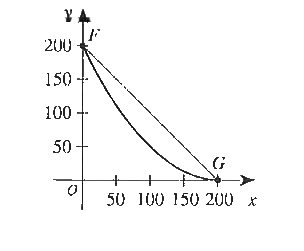
The curve y = 0.005x^(2) - 2x + 200 for 0 le x le 200 and the line segment from F(0.200) to G(200,0) are shown in the standard (x,y) coordinate plane below. Tran wants to approximate the area underneath the curve y = 0.005 x^(2) - 2x + 200 for 0 le x le 200, shown shaded in the graph below. He finds an initial estimate, A, for the shaded area by using bar(FG) and computing A = 1/2(200 units) (200 units) = 20,000 square units. The area of the shaded region is:
Tran wants to approximate the area underneath the curve y=0.005x2−2x+200 for 0≤x≤200, shown shaded in the graph below.
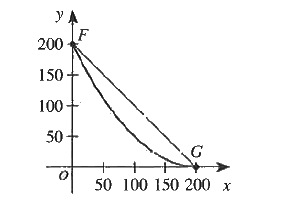
ocr_image
He finds an initial estimate, A, for the shaded area by using ¯¯¯¯¯¯FG and computing A=12(200units)(200units)=20,000 square units.
The area of the shaded region is:

A

less than 20,000 square units, because the curve lies under ¯¯¯¯¯¯FG.

B

less than 20,000 square units, because the curve lies over ¯¯¯¯¯¯FG.

C

equal to 20,000 square units.

D

greater than 20,000 square units, because the curve lies under ¯¯¯¯¯¯FG.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

|
Answer

Step by step video, text & image solution for The curve y = 0.005x^(2) - 2x + 200 for 0 le x le 200 and the line segment from F(0.200) to G(200,0) are shown in the standard (x,y) coordinate plane below. Tran wants to approximate the area underneath the curve y = 0.005 x^(2) - 2x + 200 for 0 le x le 200, shown shaded in the graph below. He finds an initial estimate, A, for the shaded area by using bar(FG) and computing A = 1/2(200 units) (200 units) = 20,000 square units. The area of the shaded region is: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023
Class 12MATHSQUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    The curve y=0.005x2−2x+200 for 0≤x≤200 and the line segment from F(0,200) to G(200,0) are shown in the standard (x,y) coordinate plane below.
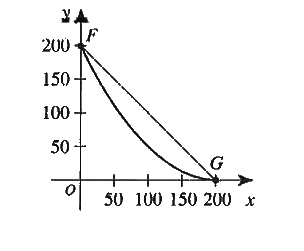
    ocr_image
    What is the y-coordinate for the point on the curve with x-coordinate 20?

    A160
    B162
    C164
    D166
  • Question 2 - Select One

    The curve y=0.005x2−2x+200 for 0≤x≤200 and the line segment from F(0.200) to G(200,0) are shown in the standard (x,y) coordinate plane below.
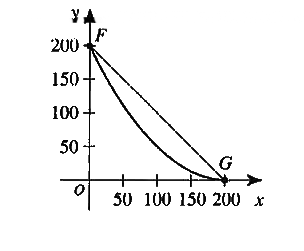
    ocr_image
    The length of this curve is longer that ¯¯¯¯¯¯FG. About how many coordinate units long is ¯¯¯¯¯¯FG?

    A20
    B141
    C200
    D283