It was observed in an experiment that the number of bacteria doubles evey hour. It was found that the number of bacteria twelve hours from the start of observation was 40960. After how many hours from the start of the experiment would the number of bacteria has been one-fourth the final number of bacteria?
11
10
8
6
The correct Answer is:B
To solve the problem step by step, we will use the information given about the bacteria doubling every hour and the final count after 12 hours.
Step 1: Understand the growth of bacteria
The number of bacteria doubles every hour. This means if we denote the initial number of bacteria as A, after n hours, the number of bacteria can be expressed as:
N(n)=A⋅2n
Step 2: Use the information given
We know that after 12 hours, the number of bacteria is 40,960. Therefore, we can set up the equation:
N(12)=A⋅212=40,960
Step 3: Solve for A
To find A, we first calculate 212:
212=4096
Now we can substitute this back into our equation:
A⋅4096=40,960
To find A, we divide both sides by 4096:
A=40,9604096=10
Step 4: Find the final number of bacteria
Now we know the initial number of bacteria A is 10. The final number of bacteria after 12 hours is:
N(12)=10⋅212=40,960
Step 5: Determine when the bacteria count is one-fourth of the final count
We need to find the time t when the number of bacteria is one-fourth of the final number:
N(t)=14⋅N(12)=14⋅40,960=10,240
Using the formula for N(t):
N(t)=A⋅2t=10⋅2t
Setting this equal to 10,240:
10⋅2t=10,240
Dividing both sides by 10:
2t=1,024
Step 6: Solve for t
Now we need to express 1,024 as a power of 2:
1,024=210
Thus, we have:
2t=210
This implies:
t=10
Conclusion
The number of bacteria will be one-fourth of the final number after 10 hours from the start of the experiment.
The number of bacteria doubles every hour. This means if we denote the initial number of bacteria as A, after n hours, the number of bacteria can be expressed as:
N(n)=A⋅2n
We know that after 12 hours, the number of bacteria is 40,960. Therefore, we can set up the equation:
N(12)=A⋅212=40,960
To find A, we first calculate 212:
212=4096
Now we can substitute this back into our equation:
A⋅4096=40,960
To find A, we divide both sides by 4096:
A=40,9604096=10
Now we know the initial number of bacteria A is 10. The final number of bacteria after 12 hours is:
N(12)=10⋅212=40,960
We need to find the time t when the number of bacteria is one-fourth of the final number:
N(t)=14⋅N(12)=14⋅40,960=10,240
Using the formula for N(t):
N(t)=A⋅2t=10⋅2t
Setting this equal to 10,240:
10⋅2t=10,240
Dividing both sides by 10:
2t=1,024
Now we need to express 1,024 as a power of 2:
1,024=210
Thus, we have:
2t=210
This implies:
t=10
The number of bacteria will be one-fourth of the final number after 10 hours from the start of the experiment.
Topper's Solved these Questions
Similar Questions
A population of bacteria doubles every 2 hours. What is the percent increase after 4 hours ?
View SolutionThe number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of 2nd hour, 4th hour and nth hour?
View Solution
Knowledge Check
A population of bacteria doubles every 2 hours . What is the percent increase after 4 hours ?
A400B500C300D600The population of a bacteria culture doubles in number every 12 minutes. The ratio of the number of bacteria at the end of 1 hour to the number of bacteria at the beginning of that hour is
A64:1B60:1C32:1D16:1As part of a laboratory experiment, the number of times a light id flashed on a certain culture of bacteria is reduced 20 percent each day. If the light flashed 704 times on the fourth day of the experiment, then the number of times it flashed on the first day is closest to
A880B1,217C1,267D1,375
The number of bacteria in a certain culture doubles every hour. If there were 30 bacteria present in the culture originally, how many bacteria will be present at the end of 2nd hour, 4th hour and nth hour?
View SolutionThe rate of increase of the bacteria in a culture is proportional to the number of bacteria present and it is found that the number doubles in 6 hours. Prove that the bacteria becomes 8 times at the end of 18 hours.
View SolutionA biologist places a colony consisting of 5000 bacteria into a petri dish. After the intial placement of the bacteria at time t = 0, the biologist measures and estimates the number of bacteria present every half hour. This data was then fitted by an exponential curve of the form y=c.2kt where c and k are constants, t is measured in hours, and y is measured in thousands of bacteria. The scatterplot together with the exponential curve are shown below.
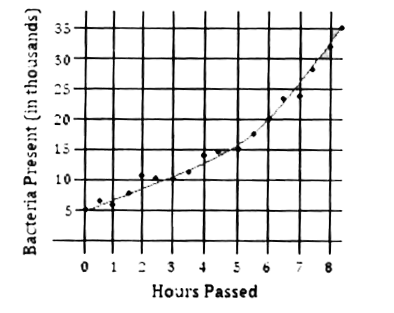
According to the scatterplot, the biologist'smeasurements indicate that the number of bacteria present quadrupled in 6 hours, and the exponential curve passes through the corresponding data point at time t = 6. The exponential function also agrees with the initial number of bacteria. Compute ck.
View SolutionThe rate of increase in the number of bacteria in a certain bacteria culture is proportional to the number present. Given the number triples in 5 hrs., find how many bacteria will be present after 10 hours. Also find the time necessary for the number of bacteria to be 10 times the number of initial present. [Given loge3=1.0986, e2.1972=9 ]
View SolutionIn a certain culture the number of bacteria at any instant increases at a rate proportional to the cube root of the number present at that instant. If the number becomes 8 times in 3 hours, when will the number be 64 times?
View Solution
