The price of coffee rose by 20% following shortange in availability in the market. As a result , Carlose decided to mitigate increasing expenses by reducing his coffee intake. By what percentage should Carlos reduce his intake so that there is no effect on the expenditure on coffe ?
0.05
0.1667
0.2
0.25
The correct Answer is:B
To solve the problem step by step, we will follow these calculations:
Step 1: Define the Initial Variables
Let the initial price of coffee per pack be X1 and the initial number of packs Carlos buys be Y1.
Step 2: Calculate the New Price After the Increase
The price of coffee rose by 20%. Therefore, the new price X2 can be calculated as:
X2=X1+(20100×X1)=X1+0.2X1=1.2X1
Step 3: Set Up the Expenditure Equation
Carlos wants to keep his expenditure the same before and after the price increase. The initial expenditure is:
Initial Expenditure=X1×Y1
The final expenditure after the price increase will be:
Final Expenditure=X2×Y2
Setting these equal gives us:
X1×Y1=X2×Y2
Step 4: Substitute the New Price into the Expenditure Equation
Substituting X2=1.2X1 into the expenditure equation:
X1×Y1=1.2X1×Y2
Step 5: Cancel X1 from Both Sides
Assuming X1 is not zero, we can divide both sides by X1:
Y1=1.2×Y2
Step 6: Solve for Y2
Rearranging gives:
Y2=Y11.2=Y165=5Y16
Step 7: Calculate the Reduction in Intake
The reduction in intake is:
Reduction=Y1−Y2=Y1−5Y16=Y16
Step 8: Find the Percentage Reduction
The percentage reduction in intake is given by:
Percentage Reduction=ReductionY1×100=Y16Y1×100=16×100≈16.67%
Conclusion
Carlos should reduce his coffee intake by approximately 16.67% to maintain the same expenditure.
---
Let the initial price of coffee per pack be X1 and the initial number of packs Carlos buys be Y1.
The price of coffee rose by 20%. Therefore, the new price X2 can be calculated as:
X2=X1+(20100×X1)=X1+0.2X1=1.2X1
Carlos wants to keep his expenditure the same before and after the price increase. The initial expenditure is:
Initial Expenditure=X1×Y1
The final expenditure after the price increase will be:
Final Expenditure=X2×Y2
Setting these equal gives us:
X1×Y1=X2×Y2
Substituting X2=1.2X1 into the expenditure equation:
X1×Y1=1.2X1×Y2
Assuming X1 is not zero, we can divide both sides by X1:
Y1=1.2×Y2
Rearranging gives:
Y2=Y11.2=Y165=5Y16
The reduction in intake is:
Reduction=Y1−Y2=Y1−5Y16=Y16
The percentage reduction in intake is given by:
Percentage Reduction=ReductionY1×100=Y16Y1×100=16×100≈16.67%
Carlos should reduce his coffee intake by approximately 16.67% to maintain the same expenditure.
Topper's Solved these Questions
Similar Questions
The price of sugar goes up by 20%. By how much percent must a hours wife reduce her consumption so that the expenditure does not increase?
View SolutionThe price of petrol rose by 10%. By how consumption should be reduced so that expenditure does not increase.
View SolutionA flowerist buys 100 dozen roses at Rs 2 a dozen. By the time the flowers are delivered, 20 dozen roses are mutilated and are thrown away. At what price should he sell the rest if he needs to make a 20% profit on his purchase?
View SolutionQuestion 37 and 38 refer to the following information
The U.S. federal Government tracks the Consumer Price Index (CPI)- a comprehensive standard used to estimate the average price change for the typical goods and services purchased by consumers. This measure gives economics a useful way to estimate the rates of the inflation or deflation, which reflects the respective general increase or decrease of prices of goods and services in the economy. The accompanying tables summarizes the changes in the CPI for the years 2005 through 2014, which can be assumed to be the corresponding percent rates of inflation.
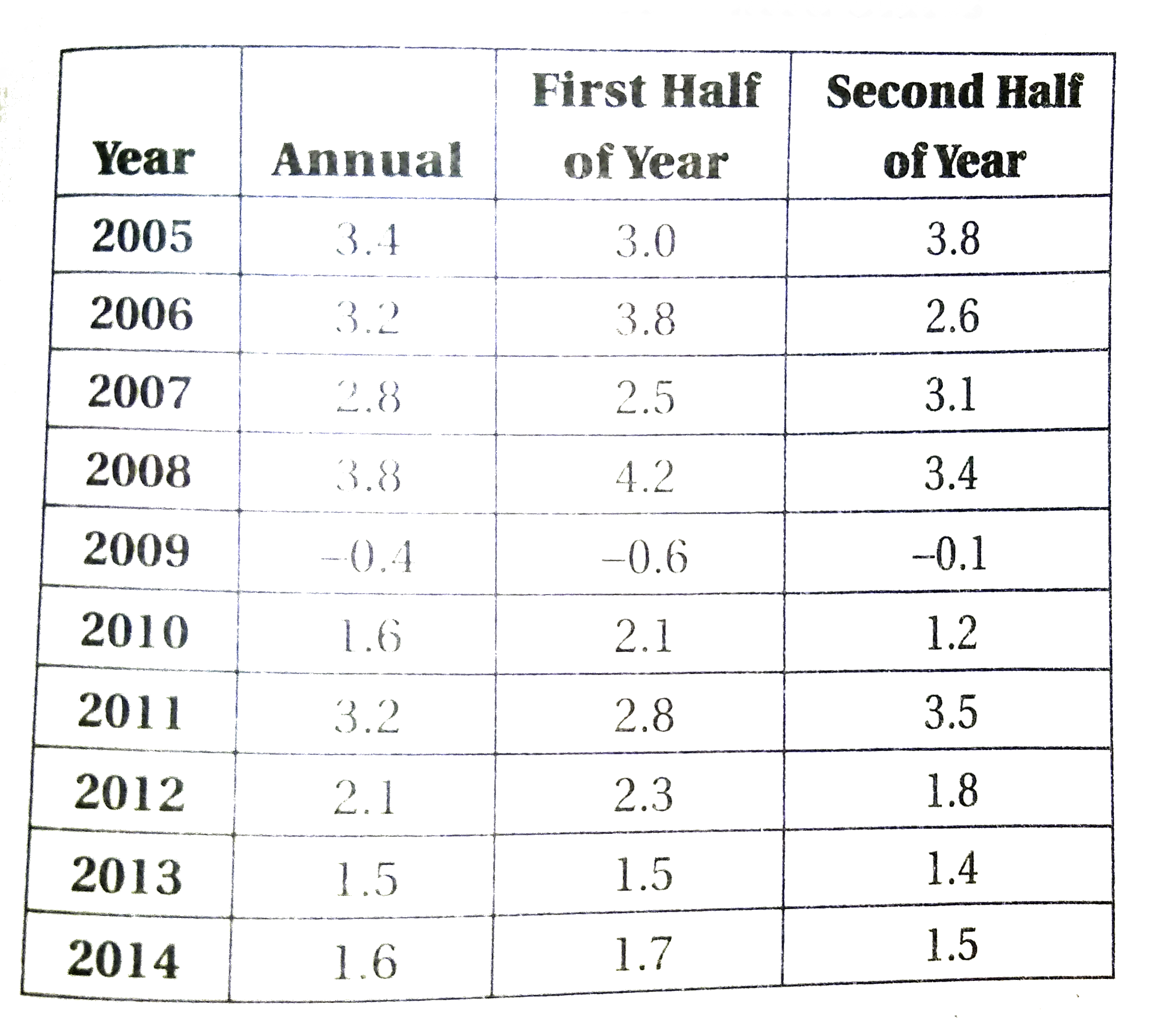
Q. At a beginning of 2015, a retired person is shopping for a retirement annunity, which is an investment policy that will give him fixed monthly payments for the rest of his life. He would like the amount of his annuity payments to more than keep up with the rate of inflation. He decides that he will choose a policy that issuse payments that increase annually at a rate of that is at least 1.5% greater than the average yearly compounded rate of inflation calculated from the period that extends from the second half of 2005 through the first half of 2008. What should be the minimum annual rate of increase in his monthly annuity payments, correct to the nearest tenth?
View Solution
