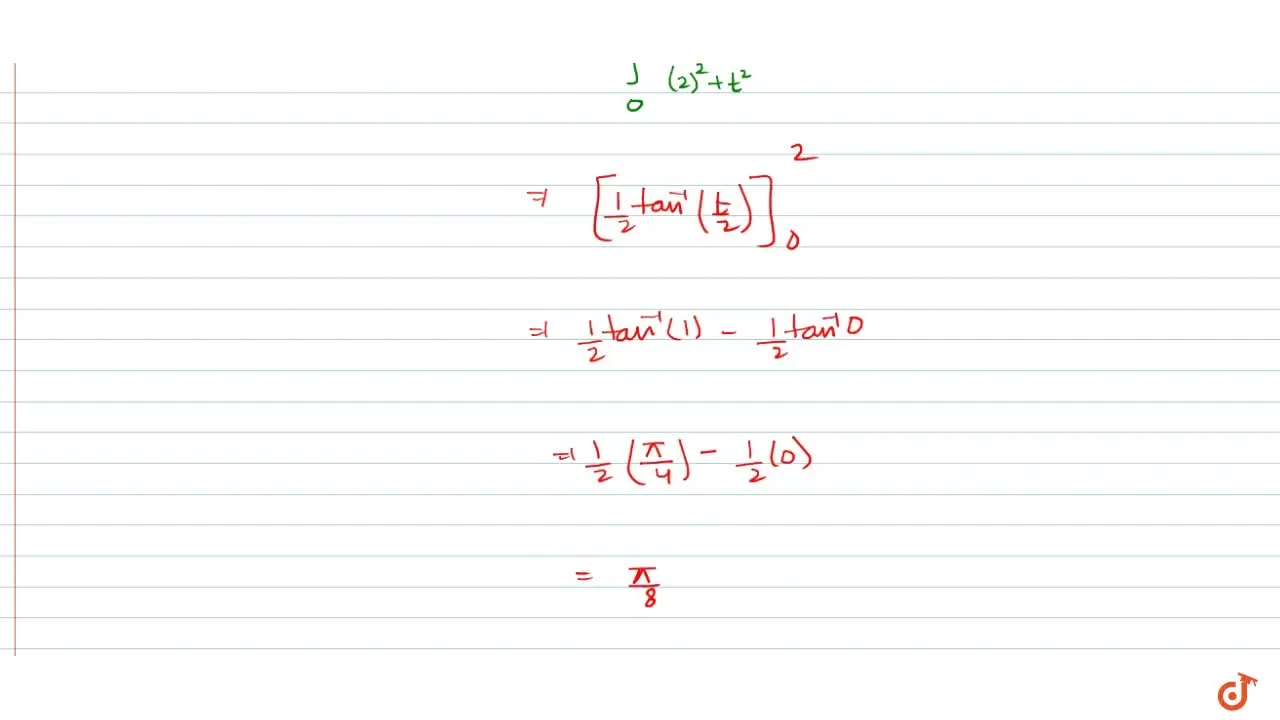Evaluate the integrals∫1−1dxx2+2x+5
Video Solution
Text Solution
Given I=∫1−1dxx2+2x+5
=∫1−1dx(x+1)2+4
=12tan−1(x+12)1−1
=12tan−1(22)−12tan−1(−1+12)
=12tan−1(1)−12tan−1(0)
=12(π4)−12(0)
=>π8−0=π8
|
Updated on:21/07/2023
Related Playlists
- BOOK - NCERTCHAPTER - INTEGRALSEXERCISE - EXERCISE 7.714videos
INTEGRALS
- BOOK - NCERTCHAPTER - INTEGRALSEXERCISE - EXERCISE 7.523videos
INTEGRALS
- BOOK - NCERTCHAPTER - INTEGRALSEXERCISE - EXERCISE 7.624videos
INTEGRALS
- BOOK - NCERTCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - EXERCISE 9.112videos
DIFFERENTIAL EQUATIONS
- BOOK - NCERTCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - MISCELLANEOUS EXERCISE17videos
INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
Evaluate the integrals∫1−1dxx2+2x+5
View SolutionEvaluate the integrals∫10xx2+1dx
View SolutionEvaluate the integral ∫1−1x√1−x2sin−1(2x√1−x2)dx.
View SolutionEvaluate the integrals∫21(1x−12x2)e2xdx
View SolutionEvaluate the integrals : I=∫−2−3dxx2−1 ,
View SolutionEvaluate the integral
I=∫20|1−x|dxView SolutionEvaluate the definite integrals∫10dx1+x2
View SolutionEvaluate the integral :
I=∫51(4x−1)dxView SolutionThe value of integral ∫1−1|x+2|x+2dx is
View SolutionThe value of integral ∫1−1|x+2|x+2 dx is
View Solution