A neutron makes a head-on elastic collision with a stationary deuteron. The fraction energy loss of the neutron in the collision is
16/82
8/9
8/27
23
The correct Answer is:B
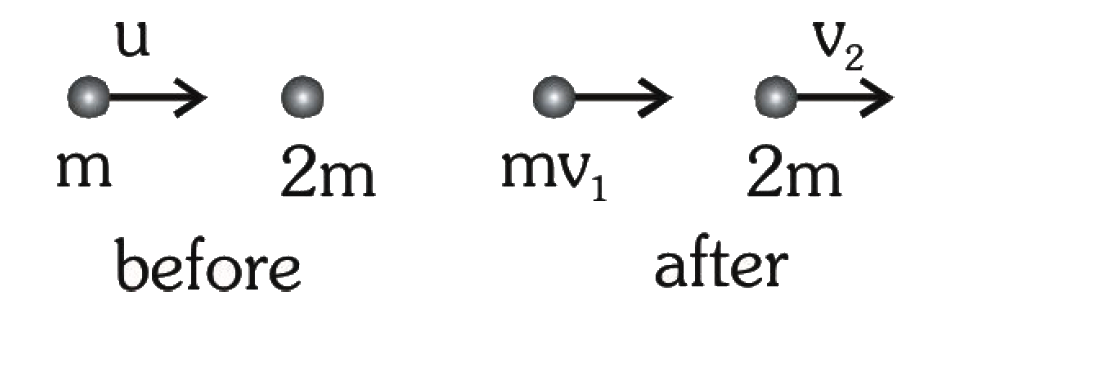
u=v1=2v2 . . . (i)
e=1−−(v1−v2)u
∴u=v2−v1 . .. (2)
solving v1=−u3,v2=2u3
fraction energy loss of neutron
12mu2−12m(−u3)212mu2=89 .
Topper's Solved these Questions
Similar Questions
A neutron collides elastically with an initially stationary deuteron. Find the fraction of the kinetic energy lost by the neutron
(a)in a head-on collision
(b) in scatterting at right angles.
View SolutionA neutron collides elastically with an initially stationary deuteron. Find the fraction of the kinetic energy lost by the neutron (a) in a head-on collision , (b) in scattering at right angles.
View Solution
Knowledge Check
A neutron makes is a head - on elastic collision with a stationary deuteron The fraction energy loss of the neutron in the collision is
A16/81B8/9C8/27D2/3In elastic collision
Aboth momentum and kinetic energy are conserved.Bboth momentum and kinetic energy are not conserved.Conly mechanical energy is conserved.Donly momentum is conserved.In elastic collision,
AK.E. and linear momentum are conserved.Blinear momentum is conservedCK.E. conservedDneither K.E. nor momentum is conserved
A neutron moving at a speed v undergoes a head-on elastic collision with a nucleus of mass number A at rest. The ratio of the kinetic energies of the neutron after and before collision is :
View SolutionIn an elastic collision
View SolutionIn an elastic collision
View SolutionA particle of mass m moving with kinetic energy K, makes a head - on elastic collision with a stationary particle of mass ηm. The maximum potential energy stored in the system during the collision is
View SolutionAn hydrogen atom moves with a velocity u and makes a head on inelastic collision with another stationary H-atom. Both atoms are in ground state before collision. The minimum value of u if one of them is to be given a minimum excitation energy is
View Solution
