Two ring of mass m and 2m are connected with a light spring and can slide over two frictionless parallel horizontal rails as shown in figure. Ring of mass m is given velocity 'v0' in horizontal direction as shown. Calculate the maximum stretch in spring during subsequent motion.

√mkv0
√3mkv0
√2m3kv0
√2mkv0
The correct Answer is:C
12kx2max=12μv20
⇒xmax=√μk.v0=√2m3kv0
Topper's Solved these Questions
Similar Questions
Two blocks of masses m and m' are connected by a light spring on a horizontal frictionless table . The spring is compressed and then released . Find the ratio of acceleration of masses .
View Solution
A block of mass 200 g is given velocity 2(m)/(s) on a horizontal surface as shown in the figure. Find the maximum compression of spring of spring constant k=100(N)/(m)View Solution
Knowledge Check
- Question 1 - Select One
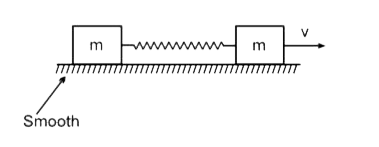
A block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
 A√2mkv0B√mk.v0C√mk.v0Dm2k.v0
A√2mkv0B√mk.v0C√mk.v0Dm2k.v0 - Question 2 - Select One
Two masses A and B of mass M and 2M respectively are connected by a compressed ideal spring. The system in placed on a horizontal frictionless table and given a velocity uˆk in the z-direction as shown in the figure. The spring is then released. In the subsequent motion the line from B to A alwyas points along the ˆi unit vector. All some instant of time mass B has a x-component of velocity as vxˆi. The velocity →vA of mass A at that instant is :-
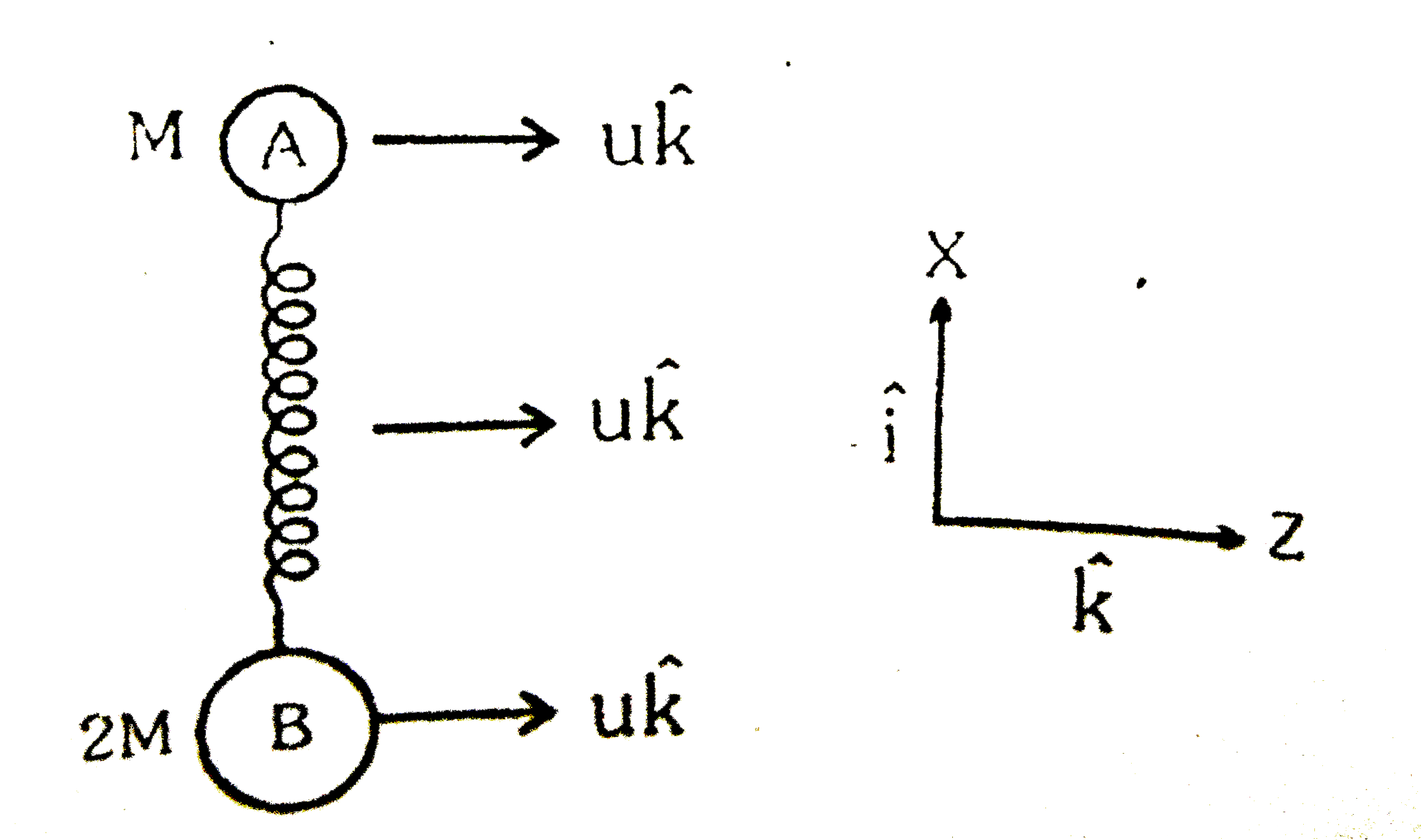 Avxˆi+uˆkB−vxˆi+uˆkC−2vxˆi+uˆkD2vxˆi+uˆk
Avxˆi+uˆkB−vxˆi+uˆkC−2vxˆi+uˆkD2vxˆi+uˆk - Question 3 - Select One
Two identical blocks of mass m, each are connected by a spring as shown in figure. At any instant of t = 0, one block is given a velocity V0 and other is given a velocity 2V0 in the same direction simultaneously as shown in figure. The maximum energy stored in spring
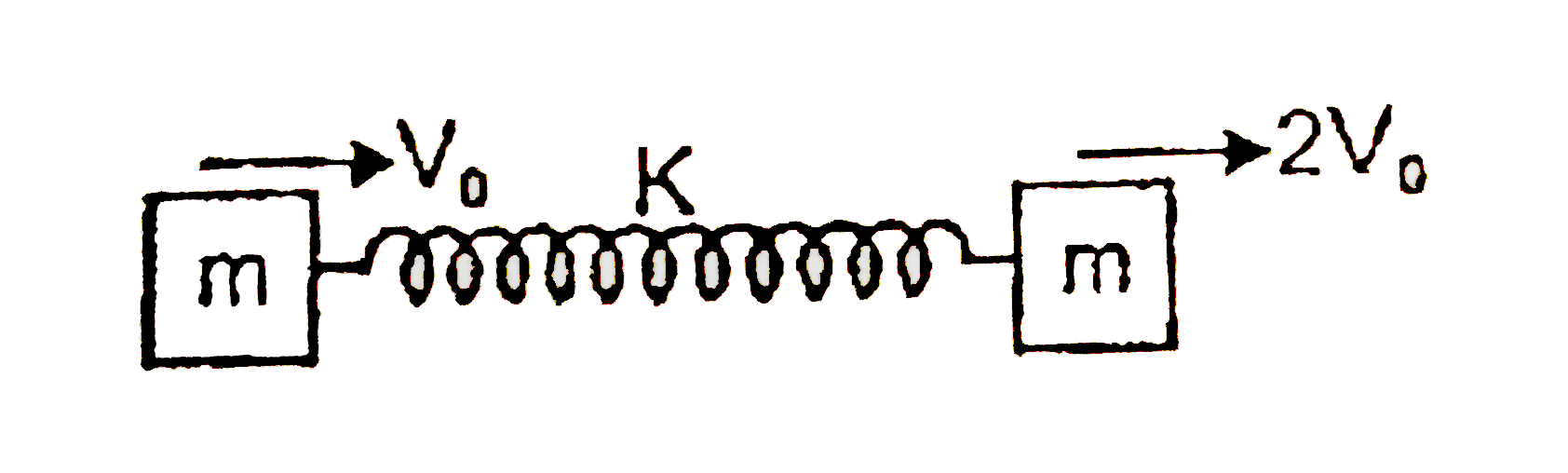 A12mV20B14mV20C34mV20D52mV20
A12mV20B14mV20C34mV20D52mV20
Two blocks each of mass m are connected over two light and frictionless pulleys and a fixed wedge by a light string as shown in figure. The tension in the string is :
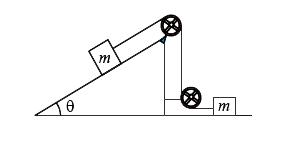 View Solution
View SolutionTwo blocks of masses m and M connected by a spring are placed on frictionless horizontal ground. When the spring is relaxed, a constant force F is applied as shown. Find maximum extension of the spring during subsequent motion.
 View Solution
View SolutionTwo masses are connected by a spring as shown in the figure. One of the masses was given velocity v = 2 k, as shown in figure where 'k' is the spring constant. Then maximum extension in the spring will be
 View Solution
View SolutionTwo blocks of mass m1 and m2 (m1<m2) are connected with an ideal spring on a smooth horizontal surface as shown in figure. At t = 0 m1 is at rest and m2 is given a velocity v towards right. At this moment, spring is in its natural length. Then choose the correct alternative :
 View Solution
View SolutionFour massless springs whose force constants are 2k, 2k, k and 2k respectively are attached to a mass M kept on a frictionless plane (as shown in figure). If the mass M is displaced in the horizontal direction, then the frequency of oscillation of the system is
 View Solution
View Solution

