The work done by 1 mole of ideal gas during an adiabatic process is (are ) given by :
P2V2−P1V1γ−1
nR(T1−T2)γ−1
P2V2−P1V1γ
None of these
The correct Answer is:A
ΔU=w=P2V1−P1V1γ−1
Topper's Solved these Questions
- THERMODYNAMICSBOOK - NARENDRA AWASTHICHAPTER - THERMODYNAMICSEXERCISE - Level 1 (Q.1 To Q.30)
6 Videos
- THERMODYNAMICSBOOK - NARENDRA AWASTHICHAPTER - THERMODYNAMICSEXERCISE - Level 1 (Q.31 To Q.60)
2 Videos
- STOICHIOMETRYBOOK - NARENDRA AWASTHICHAPTER - STOICHIOMETRYEXERCISE - Level 3 - Subjective Problems
20 Videos
Similar Questions
Define an adiabatic process and state essential conditions for such a process to take place. Write its process equations in terms of , and . Show analytically that work done by one mole of an ideal gas during adiabatic expansion from temperature T1 to T2 is given by =R(T1−t2)1−λ.
View SolutionWork Done In Adiabatic Process
View Solution
Knowledge Check
The ideal gas equation for an adiabatic process is
APVγ=constantBTVγ+1=constantCPγ−1=constantDPγ+1T=constantThe work done in adiabatic process is given by
AnR(T1)−T2γBnR(T1)−T2γ−1C(nR(T1)−T2)RDγ(T1)−T2RnWORK DONE IN ADIABATIC PROCESS
AnR(T1−T2)γBnR(T1−T2)γ−1Cnγ(T1−T2)RDγ(T1−T2)Rn

An ideal gas undergoes a cyclic process, in which one process is isochoric, one process is isothermal and one process is adiabatic. During the isothermal process, 40 J heat is released by the gas, and during the isochoric process, 80 J heat is absorbed by the gas. if work done by the gas during adiabatic process is W1 and during isothermal process is W2 then the magnitude of W1W2 will be equal to:
View SolutionWork Done In Adiabatic Processes
View SolutionThree moles of an ideal gas undergo a cyclic process shown in figure. The work done by the gas during the process is [Take ln (2)=0.693]
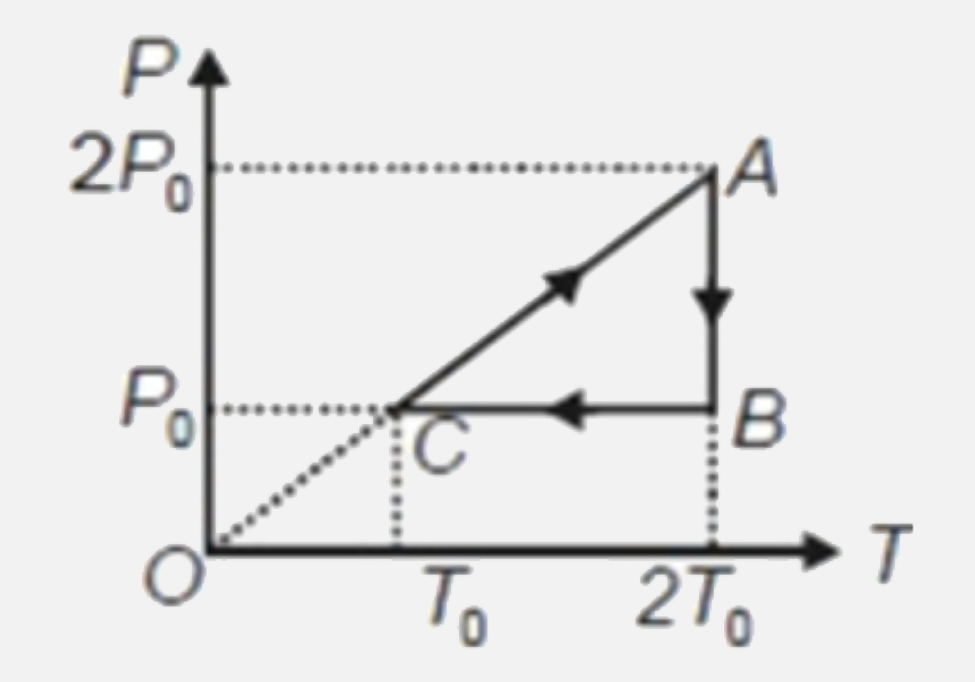
View SolutionDuring an adiabatic reversibly expansion of an ideal gas
View SolutionThe molar heat capacity C for an ideal gas going through a given process is given by C=aT, where 'a' is a constant. If γ=CpCv, the work done by one mole of gas during heating from T0 to ηT0 through the given process will be
View Solution
