$^{227} A c$ has a half-life of 22 years with respect to radioactive decay. The decay follows two prallel paths : $^{227} A c \to^{227} T h {and}^{227} A c \to^{223} F r .$ If the percentage of the two daughter nuclides are 2.0 and 98.0, respectively, the decay constant (in ${year}^{- 1}$ ) for $^{227} A c \to^{227} T h$ path is closest to

Video Solution

Text Solution

Verified by Experts

$t_{1 / 2} of A c^{227} = 21.8 y r .$
$λ = Disintegration constant = \frac{0.693}{t_{1 / 2}}$

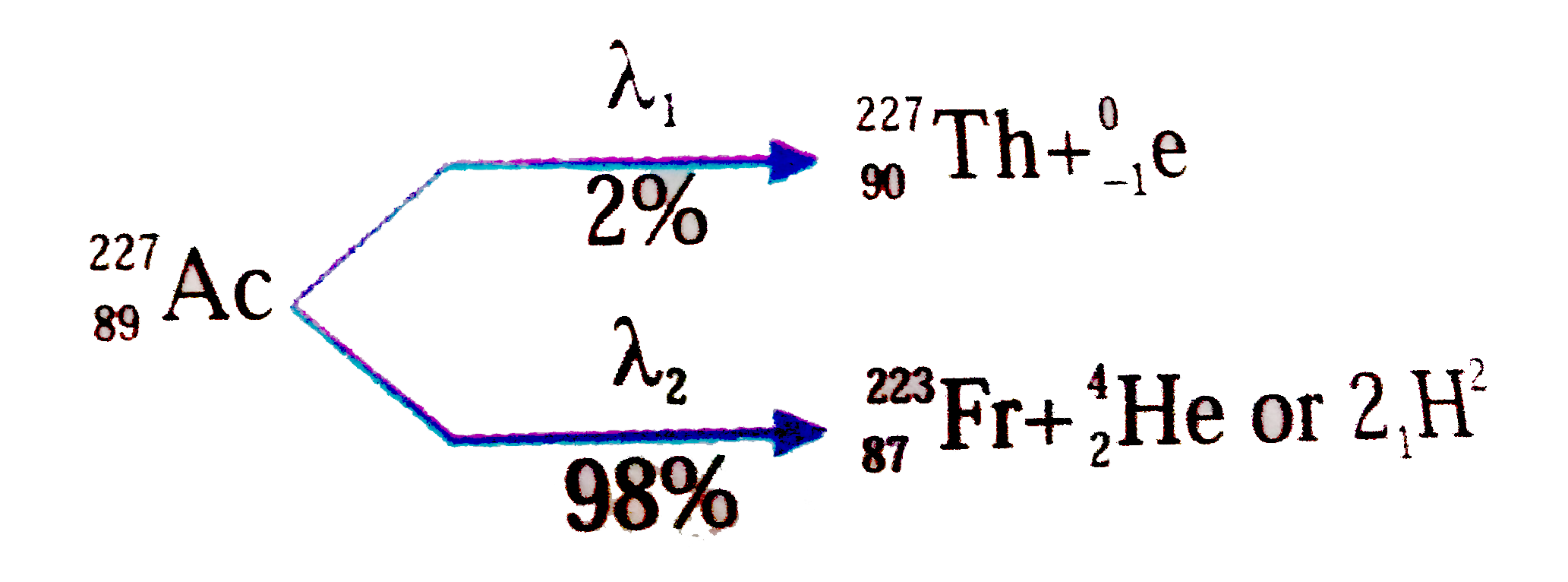
$λ = \frac{0.693}{21.8} y r^{- 1}$
$Let λ_{1} and λ_{2} are decay constant for T h^{227} and$
$F e^{223} respectively$
$λ = λ_{1} (T h) + λ_{2} (F r)$
$λ_{1} = % o f T h \times λ = \frac{2}{100} \times \frac{0.693}{21.8}$
$= \frac{0.02 \times 0.693}{21.8} y r^{- 1}$
$λ_{2} = % of F r \times λ = \frac{98}{100} \times \frac{0.693}{21.8} = 0.98 \times \frac{0.693}{21.8}$
$λ = λ_{1} + λ_{2}, N o = I n i t i a l c o n c .$
$The rate of decay of Ace to Th = [\frac{d N}{d t}]_{T h} = λ_{1} \times N_{0}$
$The rate of decay of Ace to Fr = [\frac{d N}{d t}]_{F r} = λ_{2} \times N_{0}$
$Since \frac{λ_{1}}{λ_{2}} = \frac{2}{98} = \frac{1}{49}$
$λ = λ_{1} + λ_{2}, λ_{2} = 49 λ_{1}$
$\frac{0.693}{21.8} = λ_{1} + 49 λ_{1} = 50 λ_{1}$
$λ_{1} = \frac{0.693}{21.8 \times 50} = 6.3 \times 10^{- 4} y e a r^{- 1}$
$λ_{2} = 49 λ_{1} = 49 \times 6.3 \times 10^{- 4}$
$= 3.087 \times 10^{- 2} y e a r^{- 1}$

Updated on:21/07/2023

$A c^{227}$ has a half-life of 22 years . The decays follows two parallel paths

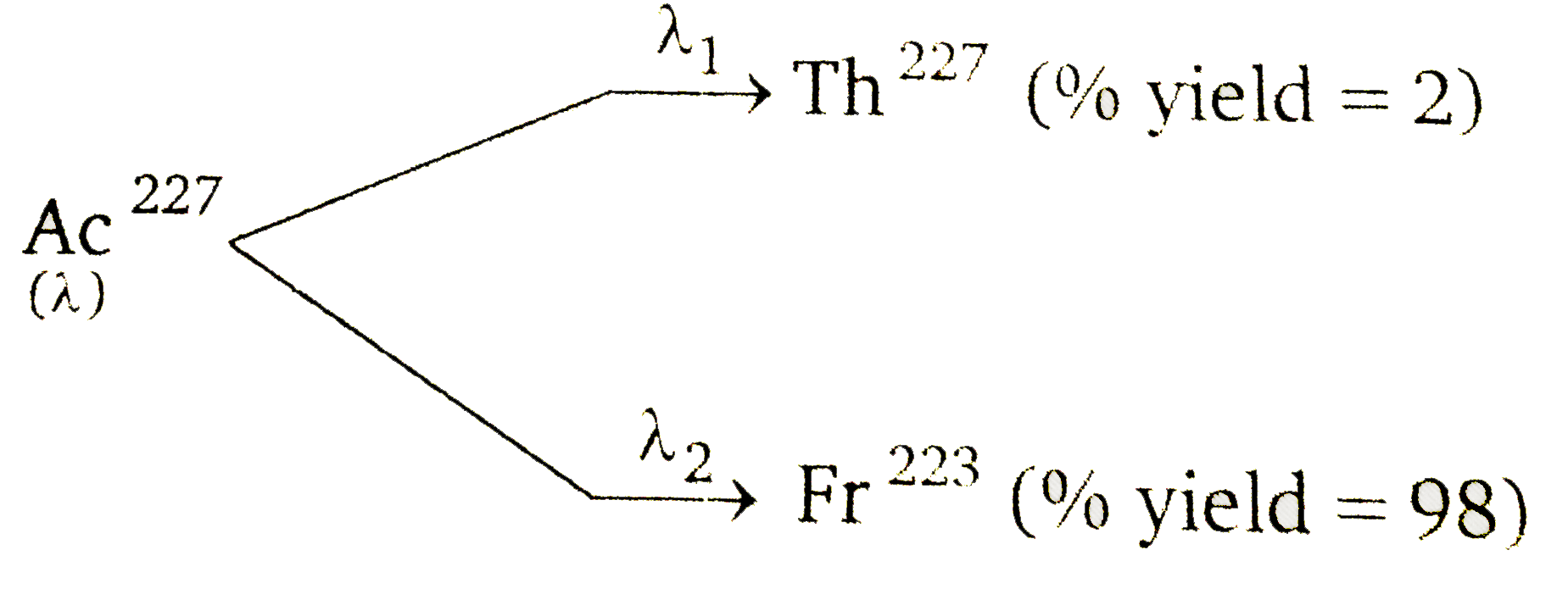
What are the decay constant $(λ)$ for Th and Fr respectively ?
A0.03087,0.00063
B0.00063,0.03087
C0.02,0.98
DNone of these
If half lives of a radioactive element, undergoing parallel path $α - decay$ and $α - decay$ are 4 years and 12 years respectively, then percentage of element that remains after 12 years will be:
A0.5
B0.125
C0.0625
D0.25
A radioactive nucleus can decay by two different processes. The half lives of the first and second decay processes are $5 \times 10^{3}$ and $10^{5}$ years respectively. Then the effective half -life of the nucleus is
A $105 \times 10^{5}$ years
B4762 years
C $10^{4}$ years
D47.6 yrs