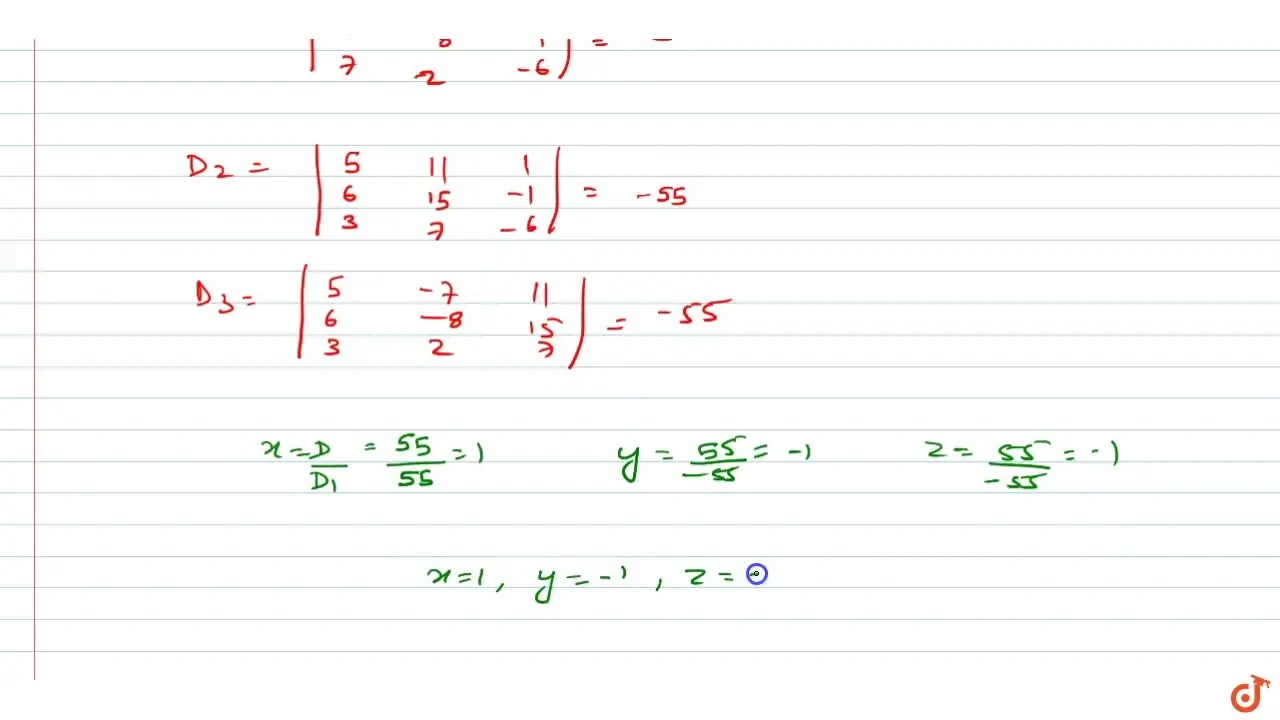Solve the following system of equations using Cramers rule. 5x−7y+z=11,6x−8y−z=15and3x+2y−6z=7
D=∣∣
∣∣5−716−8−132−6∣∣
∣∣=55
D1=∣∣
∣∣11−7115−8−172−6∣∣
∣∣=55
D2=∣∣
∣∣5111615−137−6∣∣
∣∣=−55
D3=∣∣
∣∣5−7116−815327∣∣
∣∣=−55
x=DD1=5555=1
y=55−55=−1
z=55−55=−1
x=1;y=−1;z=−1
Answer
Related Playlists
Similar Questions
Solve the following system of equations by Cramers rule 2x−y=17 , 3x+5y=6
View SolutionSolve the following system of equations, using Cramer'e rule :
x+y+3z=6, x−3y−3z=−4, 5x−3y+3z=8View SolutionSolve the following system of equations by Cramer's Rule :
x+3y=4, y+3z=7, 4x+z=6View SolutionSolve the following system of equation by Cramer's rule.
x+y+z=9
2x+5y+7z=52
2x+y-z=0View SolutionSolve the following system of linear equations by Cramers rule: 2x−y=1, 7x−2y=−7
View SolutionSolve the following system of linear equations by Cramers rule: x−2y=4, −3x+5y=−7
View SolutionSolve the following system of linear equations by Cramers rule: 2x−y=17, 3x+5y=6
View SolutionSolve the following system of equations by Cramer's Rule :
3x+y+z=10, x+y+z=0, 5x−9y=1.View SolutionSolve the following system of equations by Cramer's Rule :
x+y+z=−1, x+2y+3z=−4 , x+3y+4z=−6View SolutionSolve the following system of linear equations by Cramers rule: 5x+7y=−2, 4x+6y=−3
View Solution