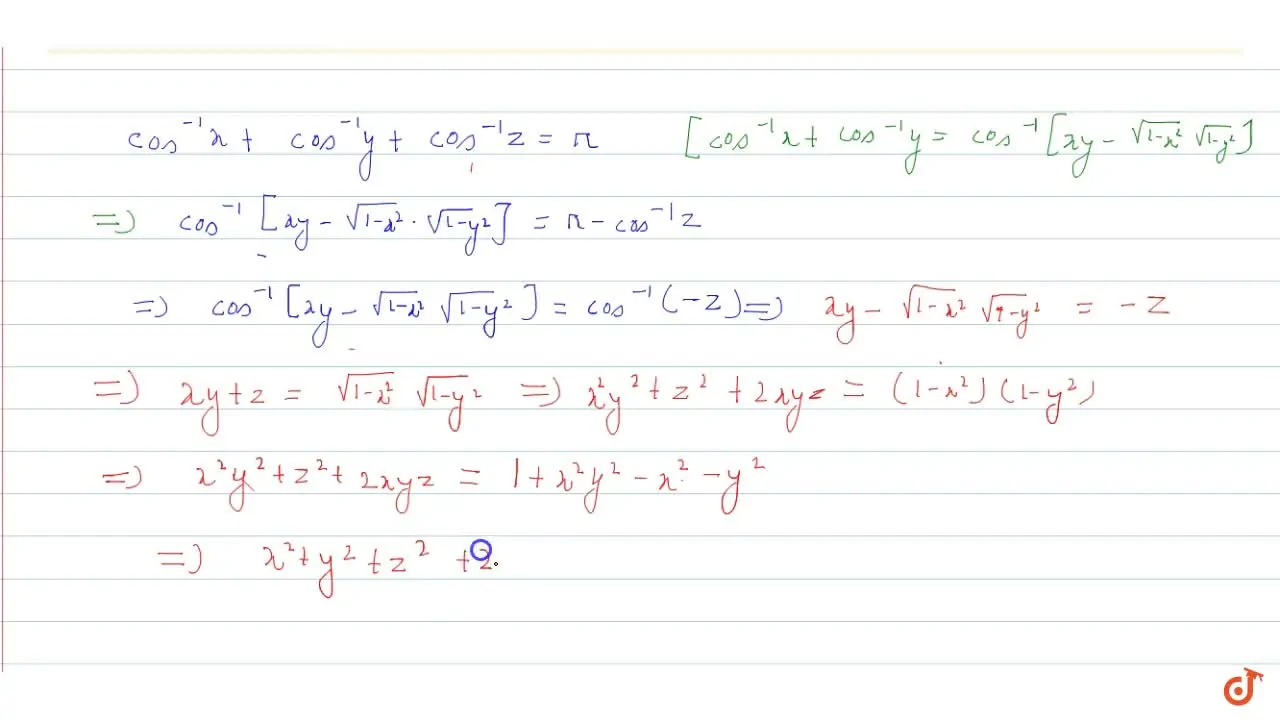If , prove that
Video Solution
Text Solution
=
=
=
=
=
=
=
|
Updated on:21/07/2023
Related Playlists
Similar Questions
If cos−1x+cos−1y+cos−1=π, prove that x2+y2+z2+2xyz=1.
View SolutionIf cos−1x+cos−1y+cos−1z=π , then
View SolutionIf cos−1x+cos−1y+cos−1z=π, then
View SolutionIf cos−1x+cos−1y+cos−1z=π , then
View SolutionIf cos−1x+cos−1y+cos−1z=π , prove that x2+y2+z2+2xyz=1.
View SolutionIf (i) cos−1x+cos−1y+cos−1z=π, prove that : x2+y2+z2+2xyz=1
(ii) If sin−1x+sin−1y+sin−1z=π2, prove that : x2+y2+z2+2xyz=1View SolutionIf cos−1x+cos−1y+cos−1z=3π then x+y+z is :
View SolutionIf cos−1x+cos−1y+cos−1z=π, then x2+y2+z2+2xyz is :
View SolutionIf cos−1x+cos−1y+cos−1z=π,then x2+y2+z2+2xyz=1 2(sin−1x+sin−1y+sin−1z)=cos−1x+cos−1y+cos−1z xy+yz+zx=x+y+z−1 (x+1x)+(y+1y)+(z+1z)≥6
View SolutionIf cos−1x+cos−1y+cos−1z=π,then x2+y2+z2+xyz=0 x2+y2+z2+2xyz=0 x2+y2+z2+xyz=1 x2+y2+z2+2xyz=1
View Solution