How many fractions will be obtained on fractional distillation of mixture of all dimethyl cyclopentance?
The correct Answer is:5
To determine how many fractions will be obtained from the fractional distillation of a mixture of all dimethyl cyclopentanes, we can follow these steps:
Step 1: Identify the Possible Isomers
We need to identify all the possible dimethyl cyclopentane isomers. Dimethyl cyclopentane can have different arrangements of the two methyl groups on the cyclopentane ring.
1. 1,1-Dimethylcyclopentane: Both methyl groups are attached to the same carbon.
2. 1,2-Dimethylcyclopentane: One methyl group is attached to one carbon, and the other methyl group is attached to an adjacent carbon.
3. 1,3-Dimethylcyclopentane: One methyl group is attached to one carbon, and the other methyl group is attached to the carbon two positions away.
4. 1,4-Dimethylcyclopentane: One methyl group is attached to one carbon, and the other methyl group is attached to the carbon directly opposite.
Step 2: Count the Unique Isomers
Now we need to determine how many of these isomers are unique and whether they can exist as enantiomers.
- 1,1-Dimethylcyclopentane: This is not chiral.
- 1,2-Dimethylcyclopentane: This can exist as two enantiomers (R and S forms).
- 1,3-Dimethylcyclopentane: This can also exist as two enantiomers (R and S forms).
- 1,4-Dimethylcyclopentane: This is not chiral.
Step 3: Calculate Total Unique Isomers
From the analysis:
- 1,1-Dimethylcyclopentane: 1 form
- 1,2-Dimethylcyclopentane: 2 forms (enantiomers)
- 1,3-Dimethylcyclopentane: 2 forms (enantiomers)
- 1,4-Dimethylcyclopentane: 1 form
So, the total number of unique isomers is:
1 (from 1,1) + 2 (from 1,2) + 2 (from 1,3) + 1 (from 1,4) = 6 unique isomers.
Step 4: Determine Fractions in Fractional Distillation
In fractional distillation, we can separate these isomers based on their boiling points. However, since enantiomers cannot be separated by this method, we consider them as one fraction each.
Thus, the fractions we can obtain from the distillation are:
- 1 fraction for 1,1-Dimethylcyclopentane
- 1 fraction for the pair of 1,2-Dimethylcyclopentane (R and S)
- 1 fraction for the pair of 1,3-Dimethylcyclopentane (R and S)
- 1 fraction for 1,4-Dimethylcyclopentane
Final Count of Fractions
So, the total number of fractions obtained from the fractional distillation of the mixture of all dimethyl cyclopentanes is:
1 + 1 + 1 + 1 = 4 fractions.
Conclusion
The answer is that 4 fractions will be obtained from the fractional distillation of a mixture of all dimethyl cyclopentanes.
---
We need to identify all the possible dimethyl cyclopentane isomers. Dimethyl cyclopentane can have different arrangements of the two methyl groups on the cyclopentane ring.
2. 1,2-Dimethylcyclopentane: One methyl group is attached to one carbon, and the other methyl group is attached to an adjacent carbon.
3. 1,3-Dimethylcyclopentane: One methyl group is attached to one carbon, and the other methyl group is attached to the carbon two positions away.
4. 1,4-Dimethylcyclopentane: One methyl group is attached to one carbon, and the other methyl group is attached to the carbon directly opposite.
Now we need to determine how many of these isomers are unique and whether they can exist as enantiomers.
- 1,2-Dimethylcyclopentane: This can exist as two enantiomers (R and S forms).
- 1,3-Dimethylcyclopentane: This can also exist as two enantiomers (R and S forms).
- 1,4-Dimethylcyclopentane: This is not chiral.
From the analysis:
- 1,1-Dimethylcyclopentane: 1 form
- 1,2-Dimethylcyclopentane: 2 forms (enantiomers)
- 1,3-Dimethylcyclopentane: 2 forms (enantiomers)
- 1,4-Dimethylcyclopentane: 1 form
1 (from 1,1) + 2 (from 1,2) + 2 (from 1,3) + 1 (from 1,4) = 6 unique isomers.
In fractional distillation, we can separate these isomers based on their boiling points. However, since enantiomers cannot be separated by this method, we consider them as one fraction each.
- 1 fraction for 1,1-Dimethylcyclopentane
- 1 fraction for the pair of 1,2-Dimethylcyclopentane (R and S)
- 1 fraction for the pair of 1,3-Dimethylcyclopentane (R and S)
- 1 fraction for 1,4-Dimethylcyclopentane
So, the total number of fractions obtained from the fractional distillation of the mixture of all dimethyl cyclopentanes is:
1 + 1 + 1 + 1 = 4 fractions.
The answer is that 4 fractions will be obtained from the fractional distillation of a mixture of all dimethyl cyclopentanes.
Topper's Solved these Questions
- ISOMERISMBook:GRB PUBLICATIONChapter:ISOMERISMExercise:MATCH THE COLUMN TYPE
Explore 22 Videos
- GASEOUS STATEBook:GRB PUBLICATIONChapter:GASEOUS STATEExercise:Exercise
Explore 530 Videos
- MOLE CONCEPT, STOICHIOMETRY & CONCENTRATION TERMSBook:GRB PUBLICATIONChapter:MOLE CONCEPT, STOICHIOMETRY & CONCENTRATION TERMSExercise:Subjective type
Explore 145 Videos
Similar Questions
Knowledge Check
Benzene is obtained by fractional distillation of
AHeavy oilBanthracene oilCMiddle oilDLight oilNumer of fractions on fractional distillation of mixture of:
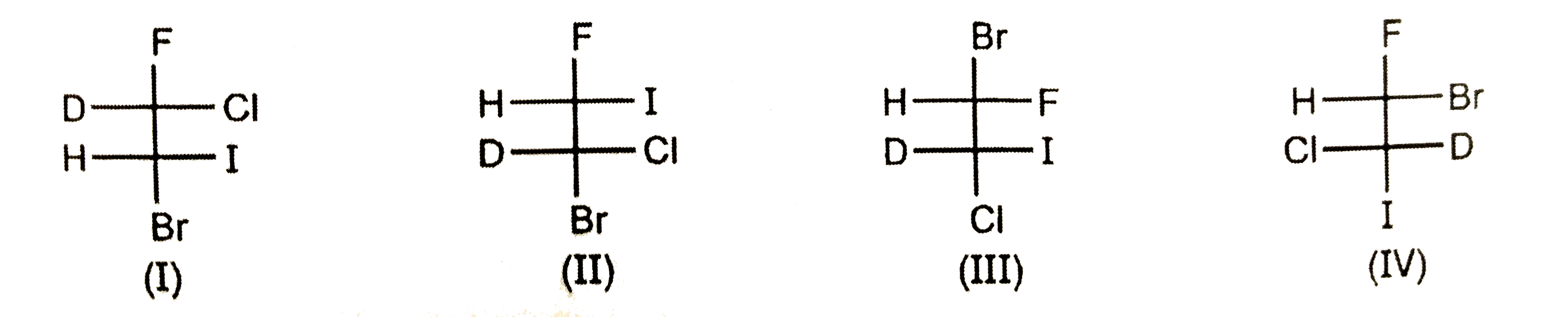 A2B3C4D1
A2B3C4D1Fractional distillation is used when
Athere is a large difference in the boiling points of liquidsBthere is a small difference in the boiling points liquidsCboiling points of liquid are sameDliquids form a constant boiling mixture
How many fractions lie between 0 and 1.
View Solution
Number of fractions obtained during fraction distillation of aM :
View SolutionDuring the fractional distillations of crude oil :
View SolutionWhat is obtained by the fraction distillation of bones?
View SolutionThe fractional distillation of coaltar yields
View Solution

