Heat capacity (CV) of an ideal gas is X KJ/mole/K. To rise its temperature from 298 K to 318 K, heat to be supplied per 10g gas will be (in KJ) [MW = 16]
16X
6.25X
32X
12.5X
The correct Answer is:D
To solve the problem of calculating the heat required to raise the temperature of 10 grams of an ideal gas with a given heat capacity, we can follow these steps:
Step 1: Identify the given values
- Heat capacity at constant volume, CV=X KJ/mole/K
- Initial temperature, T1=298 K
- Final temperature, T2=318 K
- Mass of the gas, m=10 g
- Molar mass of the gas, MW=16 g/mole
Step 2: Calculate the change in temperature (ΔT)
ΔT=T2−T1=318K−298K=20K
Step 3: Calculate the number of moles of the gas (N)
To find the number of moles, use the formula:
N=mMW=10g16g/mole=1016=58moles
Step 4: Use the formula for heat (Q)
The heat supplied can be calculated using the formula:
Q=N⋅CV⋅ΔT
Substituting the values we have:
Q=(58)⋅X⋅20
Step 5: Simplify the expression
Q=5⋅208⋅X=1008⋅X=12.5⋅XKJ
Conclusion
The heat required to raise the temperature of 10 grams of the gas from 298 K to 318 K is:
Q=12.5XKJ
- Heat capacity at constant volume, CV=X KJ/mole/K
- Initial temperature, T1=298 K
- Final temperature, T2=318 K
- Mass of the gas, m=10 g
- Molar mass of the gas, MW=16 g/mole
ΔT=T2−T1=318K−298K=20K
To find the number of moles, use the formula:
N=mMW=10g16g/mole=1016=58moles
The heat supplied can be calculated using the formula:
Q=N⋅CV⋅ΔT
Substituting the values we have:
Q=(58)⋅X⋅20
Q=5⋅208⋅X=1008⋅X=12.5⋅XKJ
The heat required to raise the temperature of 10 grams of the gas from 298 K to 318 K is:
Q=12.5XKJ
Topper's Solved these Questions
- THERMODYNAMICSBook:NARAYNAChapter:THERMODYNAMICSExercise:Level-II (H.W)
Explore 24 Videos
- THERMODYNAMICSBook:NARAYNAChapter:THERMODYNAMICSExercise:Level -V
Explore 106 Videos
- THERMODYNAMICSBook:NARAYNAChapter:THERMODYNAMICSExercise:Level-IV
Explore 27 Videos
- STRUCTURE OF ATOMBook:NARAYNAChapter:STRUCTURE OF ATOMExercise:EXERCISE - IV EXEMPLAR PROBLEMS
Explore 24 Videos
Similar Questions
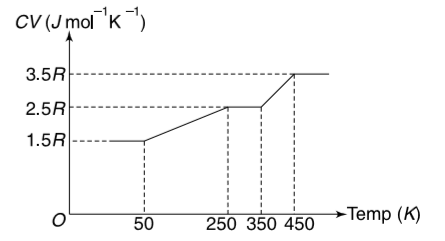
The molar specific heat capacity at constant volume (CV) for an ideal gas changes with temperature as shown in the graph. Find the amount of heat supplied at constant pressure in raising the temperature of one mole of the gas from 200 K to 400 K.
View SolutionOne mole of an ideal gas requires 207 J heat to raise its temperature by 10 K when heated at constant pressure. If the same gas is heated at constant volume to raise the temperature by the same 10 K, the heat required will be (R, the gas constant = 8.3JK−1mol−1):
View Solution
Knowledge Check
One mole of a gas absorbs 200 J of heat at constant volume. Its temperature rises from 298 K to 308 K. The change in internal energy is :-
A200 JB−200JC200×308298D200×298308JWhen 1 mole of a gas is heated at constant volume temperature is raised from 298K to 308 K heat supplied to the gas is 500J then which statement is correct?
Aq=−W=500J,δE=0Bq=W=500J,δE=0Cq=δE=500J,W=0DδE=0,q=W=−500JWhen 1 mole of a gas is heated at constant volume temperature is raised from 298K to 308 K heat supplied to the gas is 500J then which statement is correct?
Aq=−W=500J,δE=0Bq=W=500J,δE=0Cq=δE=500J,W=0DδE=0,q=W=−500J
One mole of an ideal gas is heated at constant pressure so that its temperature rises by ΔT= 72 K. In The heat supplied is Q=1.6 kJ, find the change in its internal energy and the work done by the gas.
View SolutionWhen 1 mole gas is heated at constant volume, temperature is raised from 298 to 308 K. Heat supplied to the gas in 500 J. Then, which statement is correct ?
View SolutionOne mole of an ideal monoatomic gas requires 200 J heat to increase its temperature by 10 K, when heated at constant pressure. The same gas is then heated at constant volume to increase its temperature by 10 K. What is the heat required ?
View SolutionWhen 1 mol of gas is heated at constant volume temperature is raised from 298 to 308 K. Heat supplied to the gas is 500 J. Then which statement is correct ?
View SolutionOne mole of an ideal gas requires 207J heat to raise the temperature by 10 K, when heated at constant pressure. If the same gas is heated at constant volume to raise the temperature by 10 K, then heat required is [given gas constant. R = 8.3 1/(mol -K)]
View Solution