Verify assoiativity for the following three mappings : f:N→Z0 (the set of non zero integers), g:Z0→Z and h:Q→R given by f(x)=2x,g(x)=1x and h(x)=ex.
Given that f:N⇒Z0,g:Z0⇒Q and h:Q⇒R.
gof : N⇒Q and hog :Z0⇒R
Right⇒h∘(g∘f):N⇒R and (hog) of: N⇒R
So, both have the same domains.
g∘f(x)=g(f(x))=g(2x)=12x (h∘g)(x)=h(g(x))=h(1x)=e1x ...(2)
Now,
( ho (g∘f)(x)=h(g∘f)(x)=h(12x)=e12x[ from (1)]
((h∘g)∘f)(x)=(h∘g)(f(x))=(hog)(2x)=e12x[from(2)]
⇒(h∘(g∘f))(x)=(({hog})∘f)(x),∀x∈N
So, ho (g∘f)=(h∘g) of
Hence, the associative property has been verified
Topper's Solved these Questions
Similar Questions
Verify assoiativity for the following three mappings : f:N→Z0 (the set of non zero integers), g:Z0→Z and h:Q→R given by f(x)=2x,g(x)=1x and h(x)=ex.
View Solution(A) For each of the following function f(x), verify that: ∫20f(x)dx=∫10f(x)dx+∫21f(x)dx: (i) f(x)=x+2 (ii) f(x)=x2+2 (iii) f(x)=ex (B) For each of the following pairs of function f(x) and g(x), verify that: ∫10[f(x)+g(x)]dx=∫10f(x)dx+∫10g(x)dx: (i) f(x)=1,g(x) =x2 (ii) f(x)=ex,g(x)=1
View Solution
Knowledge Check
Let f(x)=x,g(x)=1/xandh(x)=f(x)g(x). Then, h(x)=1, if
Ax is any rational numberBx is a non-zero real numberCx is a real numberDx is a rationa numberIf f∘g=g∘f, where f(x)=2x+5andg(x)=3x+h, then: h=
A5B10C15D6If f(x)=x, g(x)=√x2 and h(x)=x2x, then the set of values for which the given functions f(x), g(x) and h(x) are identical is :
AR-{0}BRCR+DR+∪{0}
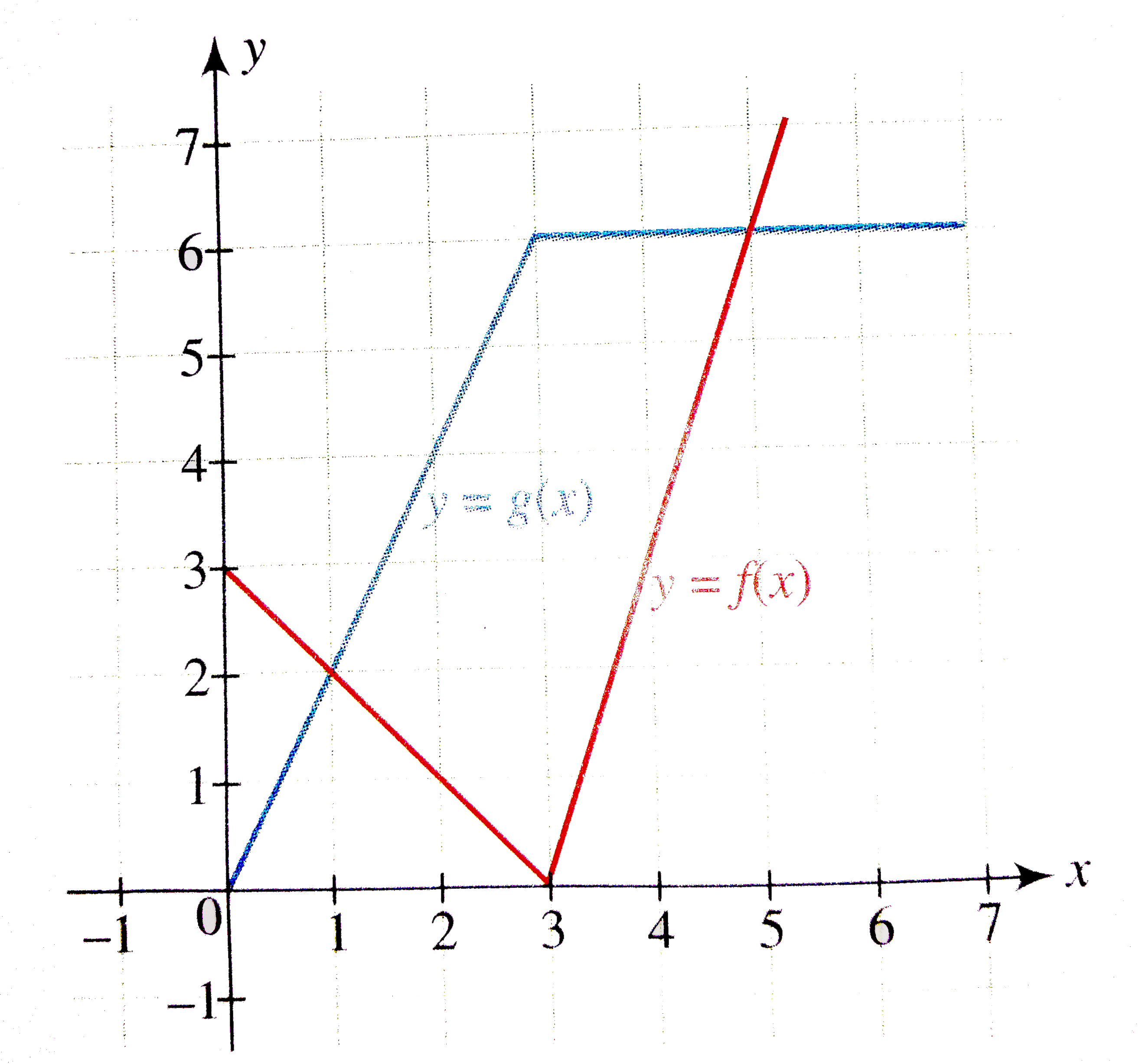
Graph of y=f(x)andy=g(x) is given in the following figure. If h(x)=f(g(x)), then find the value of h'(2).
View SolutionIf f:R→R,g,R→R be two funcitons, and h(x)=2min{f(x)−g(x),0} then h(x)=
View SolutionThe composite mapping fog of the maps f:R→R,f(x)=sinxandg:R→R,g(x)=x2, is
View SolutionIf f(x)=sinlog(√4−x21−x), then the domain of f(x) is ….
View SolutionIf f(x)=4x−5,g(x)=x2andh(x)=1x, then f(g(h(x))) is :
View Solution