रिडबर्ग सूत्र का उपयोग करते हुए हाइड्रोजन सपक्त्रम की लाइमन श्रेणी में प्रथम चार स्पेक्रामि रेखाओं के तरंगदैधर्य को परिकलित लीजिए |
रिडबर्ग का सूत्र है -
1λ=R(1n21−1n22)
जहाँ, R=1.097×107m−1
लाइमन श्रेणी के लिए n1=1
∴1λ=R(112−1n2) जहाँ, n = 2, 3, 4, 5, .....
=1.097×107(1−1n2)
=1.097×107(n2−1n2)
या λ=n21.097×107(n2−1) …(1)
लाइमन श्रेणी की प्रथम स्पेक्ट्रमी रेखा के लिए n = 2
∴λ=221.097×107(22−1)=4×10−71.097×3
=1.215×10−7=1215×10−10m
=1215Å.
लाइमन श्रेणी की द्वितीय स्पेक्ट्रमी रेखा के लिए n = 3
∴λ=321.097×107(32−1)=9×10−71.097×8
=1.026×10−7
1026×10−10=1026Å
लाइमन श्रेणी की तृतीय स्पेक्ट्रमी रेखा के लिए n = 4
∴λ=421.097×107(42−1)=16×10−71.097×15
=0.9723×10−7
=972.3×10−10=972.3Å
लाइमन श्रेणी की चतुर्थ स्पेक्ट्रमी रेखा के लिए n = 5
∴λ=521.097×107(52−1)=25×10−71.097×24
=0.9496×10−7
=949.6×10−10m=949.6Å.
Similar Questions
यदि हाइड्रोजन परमाणु का एक इलेक्ट्रॉन लाइमन श्रेणी में चतुर्थ उतेजित अवस्था से आद्य अवस्था में गति करता है तो स्पेक्ट्रमी रेखाओं की कूल संख्या ज्ञात कीजिए?
View Solutionहाइड्रोजन की बामर श्रेणी की प्रथम रेखा की तरंग संख्या 1520 m^(-1) है। Li^(2+) आयन की प्रथम बामर रेखा की तरंग संख्या m^(-1) में x है। x/100 का मान ज्ञात कीजिए।
View Solutionजब R _(H) 109678 cm ^(-1) है, तो लाइमन श्रेणी के हाइड्रोजन स्पेक्ट्रम में सबसे छोटी तरंगदैर्ध्य है:
View Solutionबोश प्रक्रम का उपयोग हाइड्रोजन गैस के उत्पादन के लिए किया जाता है, दी गई गैस में से किस गैस का उपयोग इसके लिए किया जाता है
View Solutionसूची I को सूची II के साथ सुमेलित कीजिए और सूची में दिए गए कोड का उपयोग करते हुए सही उत्तर का चयन कीजिए।
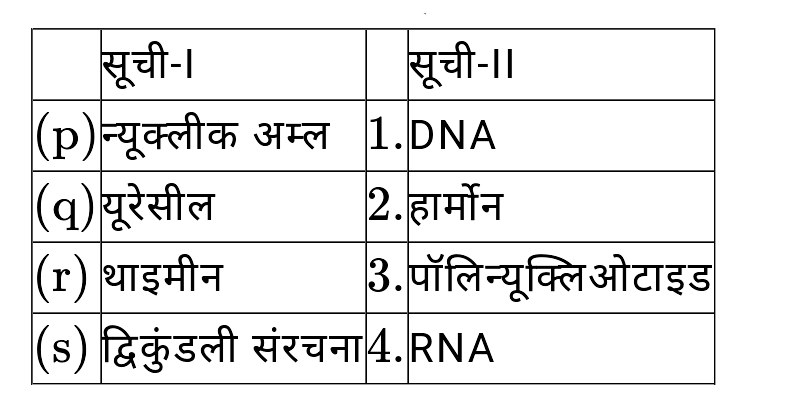
View Solutionहाइड्रोजन परमाणु के लिए, इलेक्ट्रॉन की प्रथम उत्तेजित अवस्था और तलस्थ स्तर की कक्षा के क्षेत्रफल का अनुपात क्या होगा?
View Solutionहाइड्रोजन परमाणु के लिए, इलेक्ट्रॉन की प्रथम उत्तेजित अवस्था और तलस्थ स्तर की कक्षा के क्षेत्रफल का अनुपात क्या होगा?
View Solutionसंरचना सूत्र|असंतृप्तता की कोटि|क्रियात्मक समूह को पहचानने का तरीका|सजातीय श्रेणी|वर्गीकरण|Summary
View Solution
