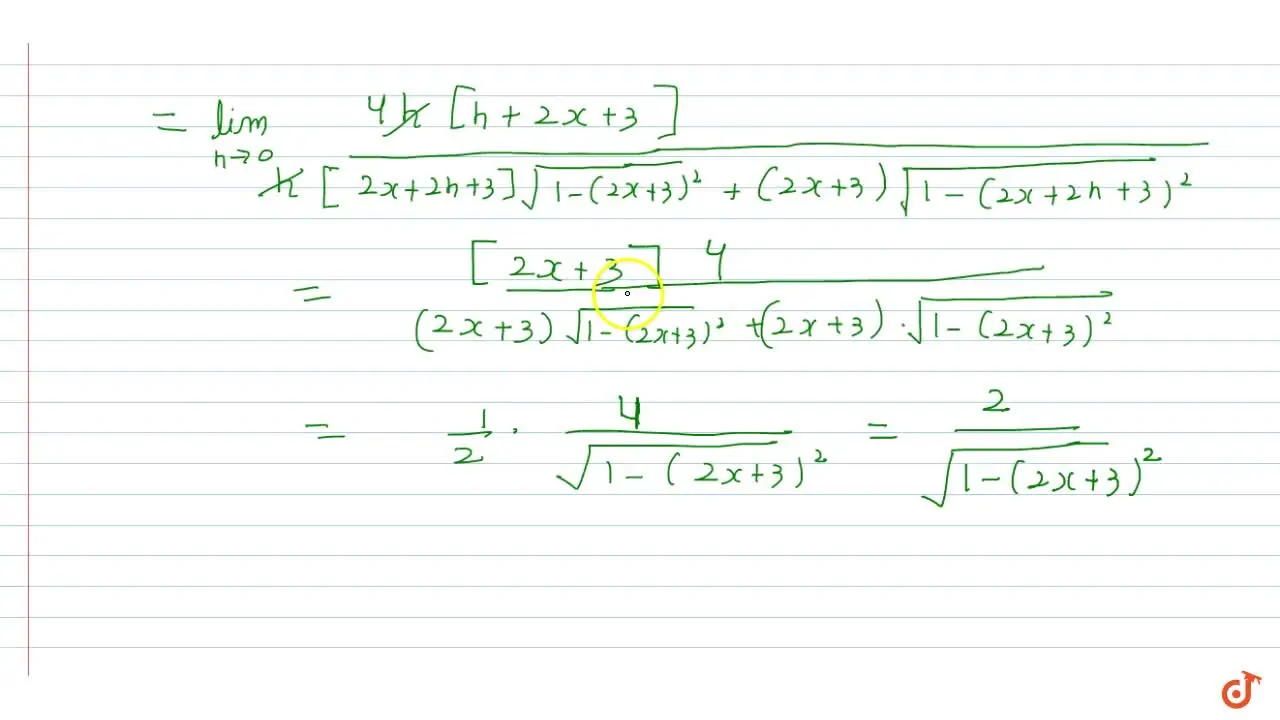Differentiate the following function from first principles:
Video Solution
Text Solution
we have
Differentiate by using first principle
.
where,
|
Updated on:21/07/2023
Related Playlists
- BOOK - RD SHARMACHAPTER - DIFFERENTIALS, ERRORS AND APPROXIMATIONSEXERCISE - Solved Examples And Exercises102videos
DIFFERENTIALS, ERRORS AND APPROXIMATIONS
- BOOK - RD SHARMACHAPTER - DIRECTION COSINES AND DIRECTION RATIOSEXERCISE - Solved Examples And Exercises67videos
DIRECTION COSINES AND DIRECTION RATIOS
Similar Questions
Differentiate the following function from first principles: e3x
View SolutionDifferentiate the following function from first principles: e−x
View SolutionDifferentiate the following function from first principles: ecosx
View SolutionDifferentiate the following function from first principles: eax+b
View SolutionDifferentiate the following function from first principles: e√cotx
View SolutionDifferentiate the following function from first principles: logcosx
View SolutionDifferentiate the following function from first principles: x2ex
View SolutionDifferentiate the following function from first principles: e√2x
View SolutionDifferentiate the following functions by first principles √sinx
View SolutionDifferentiate each of the following from first principle: −x
View Solution