A large window has the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 2 metres find the dimensions of the rectangle that will produce the largest area of the window.
Let the 2 sides be x,y
Given perimeter =2
P=3x+2y=2
y= 2−3x2
area of the window is given by,
A=xy+√34x2
A=(x(2−3x)2)+√34x2
A=x−32x2+√34x2
dAdx =1−3x+√32x
equate, dAdx =0
=1−x(3−√32)=0
x=13−√32
x=26−√3
we have,
y=1−32(26−√3)
y=3−√36−√3
d2Adx2=−(3−√32)<0
Therefore, largest area of the window is produced when sides are
26−√3,3−√36−√3m
Topper's Solved these Questions
Similar Questions
A window has the shape of a rectangle surmounted by an equilateral triangle. If the perimeter of the window is 12 m, find the dimensions of the rectangle that will produce the largest area of the window.
View Solutionlight it. surmounted b through maximum a rectangle 30. A window has the shape of an equilateral triangle. the perimeter of the window is 12m, find the dimensions of the window will produce the largest area of the window.
View SolutionA window is in the shape of a rectangle surmounted by a semi circle. If the perimeter of the window is of fixed length then the maximum area of the window is
View SolutionA window is in the form of a rectangle surmounted by a semi-circle. If the total perimeter of the window is 30\ m, find the dimensions of the window so that maximum light is admitted.
View SolutionA window is in the form of a rectangle surmounted by a semi-circular opening. The total perimeter of the window is 10 meters. Find the dimensions of the rectangle so as to admit maximum light through the whole opening.
View Solution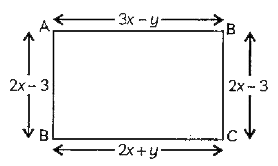
Given that the perimeter of the rectangle is 120cm, find:
the area of the rectangle.
View SolutionThe width of a rectangle is two-thirds its length. If the perimeter is 180 metres, find the dimensions of the rectangle.
View SolutionA window is in the form of a rectangle surmounted by a semicircular opening. The total perimeter of the window is 10 m. Find the dimensions of the window to admit maximum light through the whole opening.
View SolutionA window in the form of a rectangle is surmounted by a semi-circular opening. The total perimeter of the window is 10m. Find the dimensions of the rectangular part of the window to admit maximum light through the whole opening.
View SolutionThe perimeter of a rectangle is 40 cm. Find the dimensions of the rectangle if its area is maximum.
View Solution
