In a right triangle, . If , what is the value of c?
The correct Answer is:B
To solve the problem, we start with the given equation and relationships.
Step 1: Use the property of trigonometric functions
We know that in a right triangle, sinx=cosy can be rewritten using the complementary angle property:
sinx=cosy⟹x+y=90∘
Step 2: Substitute the expressions for x and y
Given x=3c+14 and y=7c+11, we can substitute these into the equation:
(3c+14)+(7c+11)=90
Step 3: Simplify the equation
Combine like terms:
3c+7c+14+11=90
10c+25=90
Step 4: Solve for c
Now, isolate c by first subtracting 25 from both sides:
10c=90−25
10c=65
Now, divide both sides by 10:
c=6510=6.5
Final Answer
Thus, the value of c is:
c=6.5
We know that in a right triangle, sinx=cosy can be rewritten using the complementary angle property:
sinx=cosy⟹x+y=90∘
Given x=3c+14 and y=7c+11, we can substitute these into the equation:
(3c+14)+(7c+11)=90
Combine like terms:
3c+7c+14+11=90
10c+25=90
Now, isolate c by first subtracting 25 from both sides:
10c=90−25
10c=65
Now, divide both sides by 10:
c=6510=6.5
Thus, the value of c is:
c=6.5
Topper's Solved these Questions
- PROBLEM SETSBook:PRINCETONChapter:PROBLEM SETSExercise:PROBLEM SET 14: FUNCTIONS
Explore 11 Videos
- PROBLEM SETSBook:PRINCETONChapter:PROBLEM SETSExercise:PROBLEM SET 15: GRID-INS
Explore 11 Videos
- PROBLEM SETSBook:PRINCETONChapter:PROBLEM SETSExercise:PROBLEM SET 12: CIRCLES, QUADRILATERALS, AND VOLUME
Explore 11 Videos
- PRACTICE TEST 4Book:PRINCETONChapter:PRACTICE TEST 4Exercise:Math Test-Calculator
Explore 38 Videos
- SAT MATH: THE BIG PICTUREBook:PRINCETONChapter:SAT MATH: THE BIG PICTUREExercise:Example
Explore 4 Videos
Similar Questions
Knowledge Check
If 7c−2b=15and3b−6c=2, what is the value of b+c ?
A−27B−3C8D17If 17x−5y=8and14x−7y=−7, what is the value of 3x+2y ?
A−15B−5C5D15If 3x+y=candx+y=b, what is the value of x in terms of c and b?
Ac−d3Bc−d2Cb−c3Db−c2
If sinx+cosy=1 and x=30∘, find the value of y.
View SolutionIf sinx+cosy=1 and x=30∘, find the value of y.
View SolutionIf sinx+cosy=1 ,x=300 and y is an acute angle. Find the value of y
View SolutionIn a right triangle ABC, right angled at C, if a = 7 cm and b = 7√3 cm, then ∠A=
View SolutionIf x=14−y, what is 3x when y=11?
View Solution
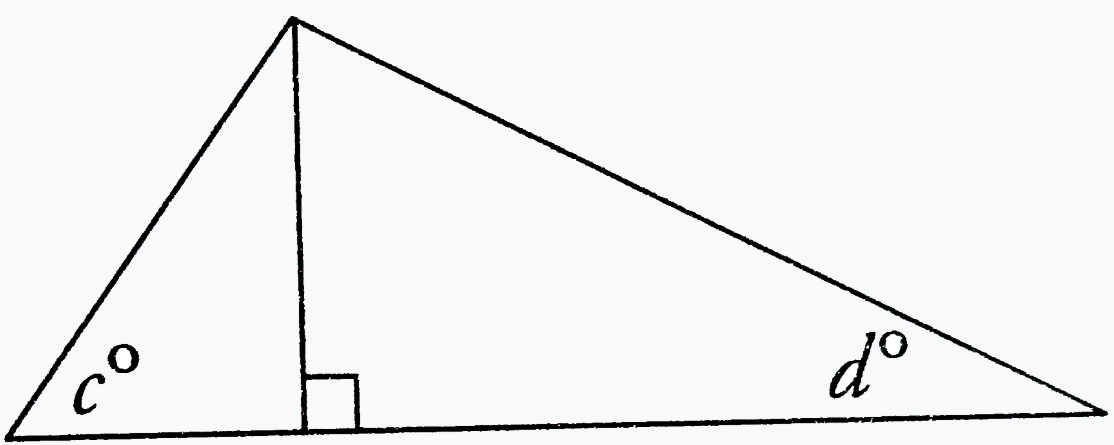 In the figure shown above,
In the figure shown above,