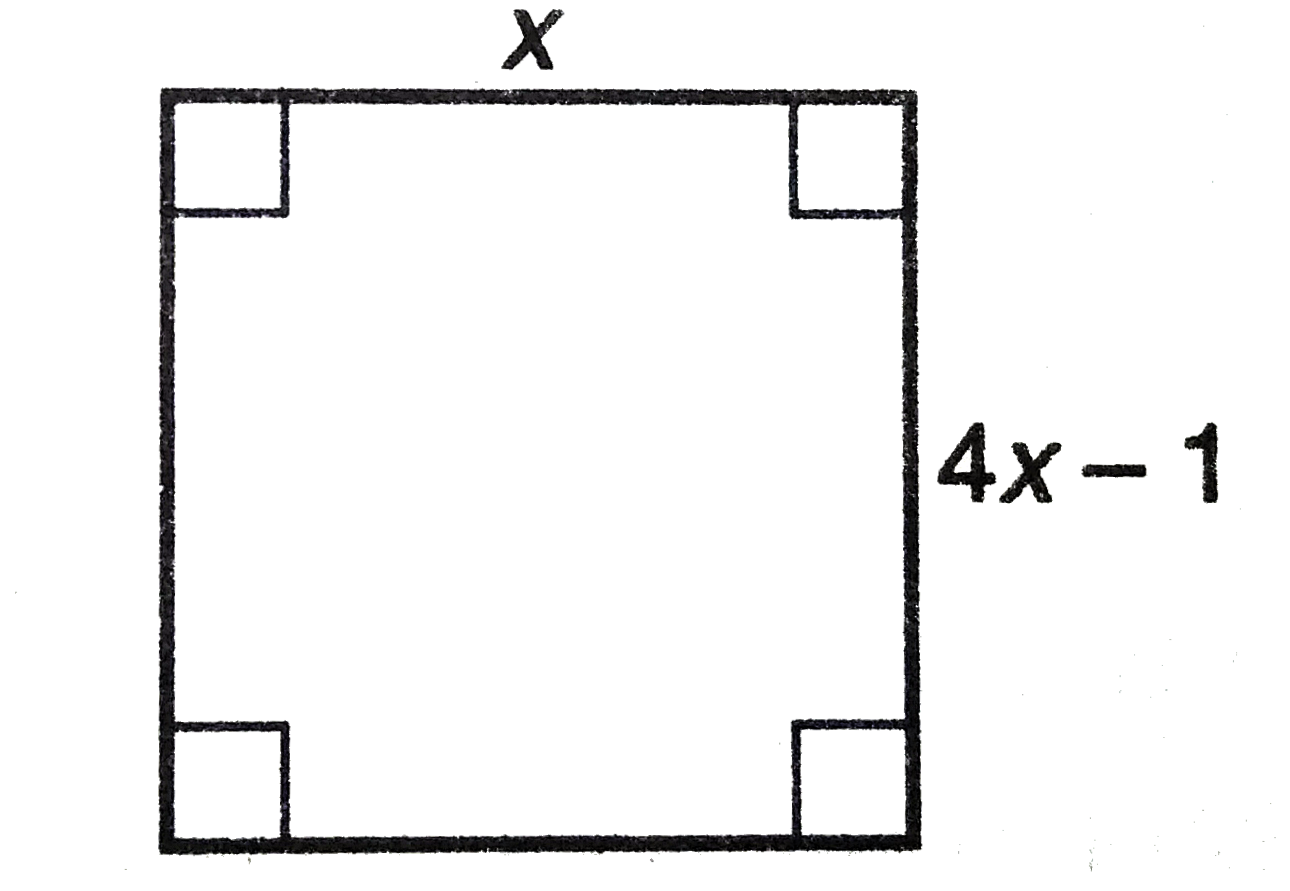
A square is inscribed in a circle with area 9z. What is the area of the square?
3√2
9√2
18
36
The correct Answer is:C
Step by step video, text & image solution for A square is inscribed in a circle with area 9z. What is the area of the square? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PROBLEM SETSBOOK - PRINCETONCHAPTER - PROBLEM SETSEXERCISE - PROBLEM SET 12: CIRCLES, QUADRILATERALS, AND VOLUME
11 Videos
- PROBLEM SETSBOOK - PRINCETONCHAPTER - PROBLEM SETSEXERCISE - PROBLEM SET 13: ADVANCED GEOMETRY
11 Videos
- PROBLEM SETSBOOK - PRINCETONCHAPTER - PROBLEM SETSEXERCISE - PROBLEM SET 10: LINES, ANGLES, AND COORDINATES
11 Videos
- PRACTICE TEST 4BOOK - PRINCETONCHAPTER - PRACTICE TEST 4EXERCISE - Math Test-Calculator
38 Videos
- SAT MATH: THE BIG PICTUREBOOK - PRINCETONCHAPTER - SAT MATH: THE BIG PICTUREEXERCISE - Example
4 Videos
Similar Questions
Knowledge Check
The side length of a square inscribed in a circle is 2. what is the area of the circle?
AπB√2πC2πD2√2πIn the figure, O is the center of the circle of radius 3, and ABCD is a square. If PC=3 and the side BC of the square is a tangent to the circle, then what is the area of the square ABCD?
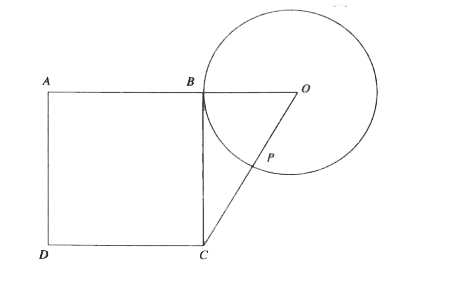 A25B27C36D42
A25B27C36D42ABCD is a square and one of its sides AB is also a chord of the circle as shown in the figure. What is the area of the square?
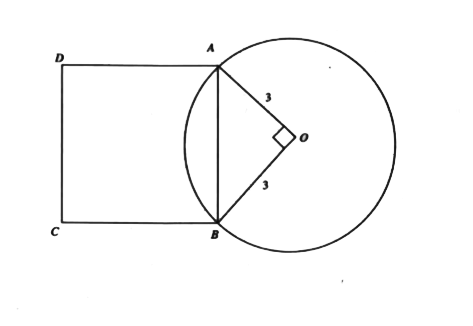 A3B9C12D18
A3B9C12D18
If a square is inscribed in a circle, find the ratio of the areas of the circle and the square.
View SolutionIf a square is inscribed in a circle, what is the ratio of the areas of the circle and the square?
View SolutionA square is inscribed in a circle. The area of the square is what percent of the area of the circle? (Disregard the percent symbol when gridding your answer).
View SolutionA square is inscribed in circle of radius R, a circle is inscribed in the square, a new square in the circle and so on for n times.
Sum of the areas of all circles is
View SolutionIn figure, a square of diagonal 8 cm is inscribed in a circle. Find the area of the shaded region.

View Solution