A toy pyramid (not shown) is made from poly(methyl methacrylate), better known by its trade term Lucite. The toy pyramid has a regular hexagonal base of 15cm2 and a height of 4 cm. In the base of the pyramid, there is a semispherical indentation 2 cm in diameter. If the pyramid weighs 21.129 g, then what is the density of Lucite? (Density equals mass divided by volume).
1.06 g/cm3
1.18 g/cm3
2.0 g/cm3
6.51 g/cm3
The correct Answer is:B
To find the density of the Lucite toy pyramid, we need to calculate the volume of the pyramid and then subtract the volume of the semi-spherical indentation. Finally, we will use the mass of the pyramid to find the density.
1. Identify the Given Information:
- Area of the base of the pyramid (A) = 15 cm²
- Height of the pyramid (h) = 4 cm
- Diameter of the semi-spherical indentation = 2 cm
- Mass of the pyramid (m) = 21.129 g
2. Calculate the Volume of the Pyramid:
The formula for the volume V of a pyramid is given by:
V=13×Area of base×Height
Substituting the values:
V=13×15cm2×4cm=13×60cm3=20cm3
3. Calculate the Volume of the Semi-Spherical Indentation:
The formula for the volume Vs of a sphere is:
Vs=23πr3
First, we need to find the radius r:
r=Diameter2=2cm2=1cm
Now substituting the radius into the volume formula:
Vs=23π(1cm)3=23π≈2×3.143≈2.094cm3
4. Calculate the Effective Volume of the Toy Pyramid:
The effective volume Ve of the toy pyramid is:
Ve=V−Vs=20cm3−2.094cm3≈17.906cm3
5. Calculate the Density of Lucite:
The density ρ is given by the formula:
ρ=MassVolume=mVe
Substituting the values:
ρ=21.129g17.906cm3≈1.18g/cm3
Final Answer:
The density of Lucite is approximately 1.18g/cm3.
---
- Area of the base of the pyramid (A) = 15 cm²
- Height of the pyramid (h) = 4 cm
- Diameter of the semi-spherical indentation = 2 cm
- Mass of the pyramid (m) = 21.129 g
The formula for the volume V of a pyramid is given by:
V=13×Area of base×Height
Substituting the values:
V=13×15cm2×4cm=13×60cm3=20cm3
The formula for the volume Vs of a sphere is:
Vs=23πr3
First, we need to find the radius r:
r=Diameter2=2cm2=1cm
Now substituting the radius into the volume formula:
Vs=23π(1cm)3=23π≈2×3.143≈2.094cm3
The effective volume Ve of the toy pyramid is:
Ve=V−Vs=20cm3−2.094cm3≈17.906cm3
The density ρ is given by the formula:
ρ=MassVolume=mVe
Substituting the values:
ρ=21.129g17.906cm3≈1.18g/cm3
The density of Lucite is approximately 1.18g/cm3.
Topper's Solved these Questions
- GEOMETRYBook:PRINCETONChapter:GEOMETRYExercise:EXAMPLES
Explore 13 Videos
- GEOMETRYBook:PRINCETONChapter:GEOMETRYExercise:Geometry Drill 1: No calculator Section
Explore 4 Videos
- GEOMETRYBook:PRINCETONChapter:GEOMETRYExercise:Geometry Drill 1: No calculator Section
Explore 4 Videos
- FUNCTIONS AND GRAPHSBook:PRINCETONChapter:FUNCTIONS AND GRAPHSExercise:Functions and Graphs Drill 2: Calculator -Permitted Section
Explore 6 Videos
- GRID-INSBook:PRINCETONChapter:GRID-INSExercise:Grid-In Drill 2: Calculator-Permitted Section
Explore 6 Videos
Similar Questions
A wooden toy is in the form of a cone surmounted on a hemisphere. The diameter of the base of the cone is 5cm and its height is 4cm. Find the cost of painting the toy at the rate of Rs. 5 per 1000cm2.
View Solution
The figure above shows a metal triangular solid with two equilateral triangle faces and a thickness of 2 cm. The length of each side of a triangular face is 4 cm. A hole with a diameter of 1 cm is drilled through the solid. The density of the metal is 6 grams per cubic centimeter . What is the mass of this solid to the nearest gram ? (Density is mass divided by volume ).
View Solution
The head of a copper ''hexagon head screw bolt'' (one cross section of which is shown above) has the shape of a cylinder with a hole shaped like a regular hexagon. The cylindrical head is 2 cm thick with a base diameter of 3 cm. The hexagonal hole is only half the thickness of the entire head, and each side of a hexagonal cross section has a length of 1 cm. Given that the density of copper is 8.96 grams per cubic cm, and density is mass divided by volume, find the mass of the head to the nearest gram.
View Solution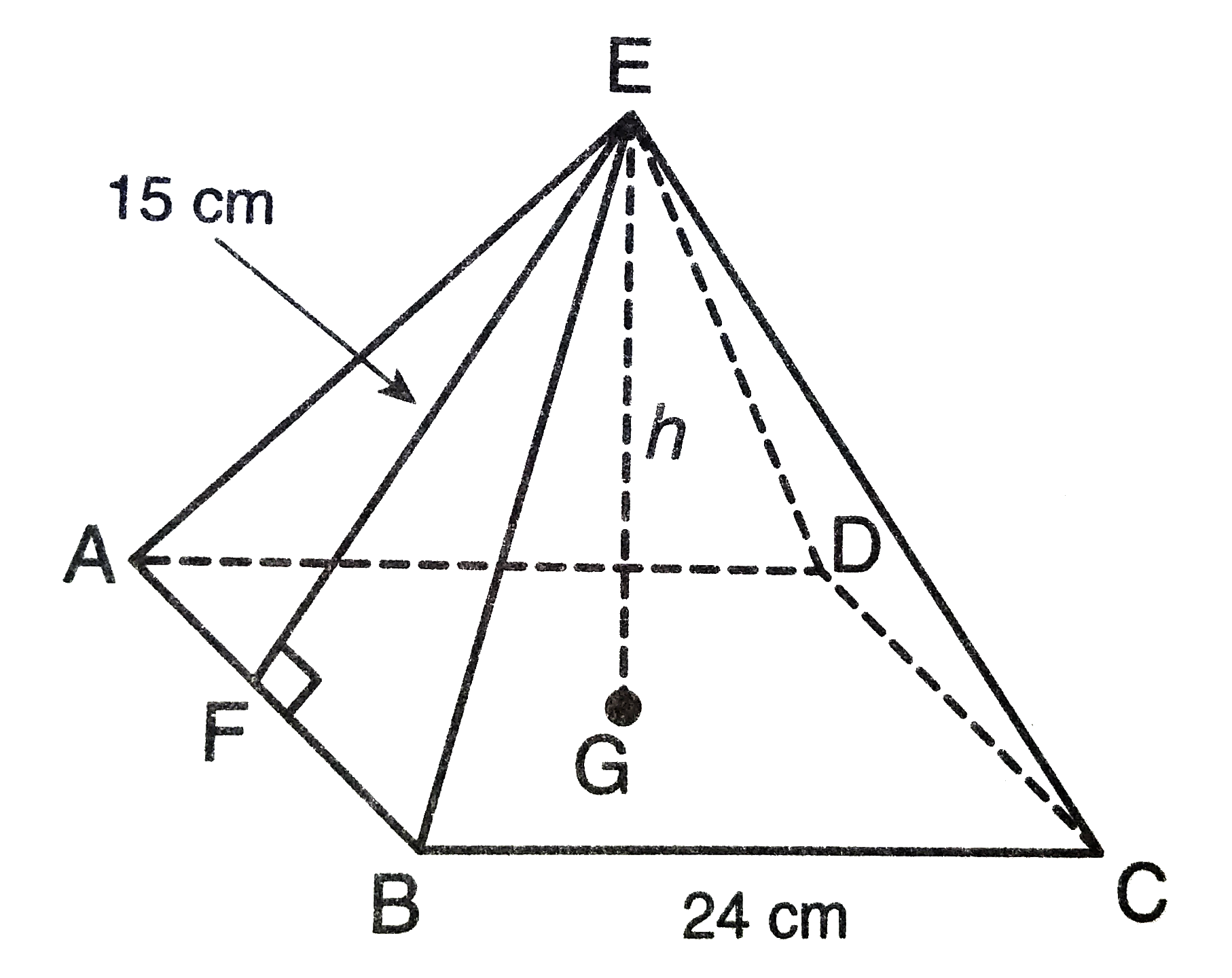
The slant height of a pyramid is the perpendicular distance from the vertex of the pyramid to the base of a figure above, the height is labeled h, the length of a side of the square base is 24 cm, and the slant height is 15 cm, What is the volume , in cubic centimeters, of the pyramid?
View SolutionA wooden toy is in the form of a cone surmounted on a hemisphere. The diameter of the base of the cone is 16cm and its height is 15cm. Find the cost of painting the toy at Rs.7 per 100 cm2.
View SolutionA company packages its milk powder in cylindrical container whose base has a diameter of 14 cm and height 20 cm. Company places a label around the surface of the container (as shown in the figure). If the label is placed 2 cm from top and bottom, what is the area of the label.
View SolutionA company packages its milk powder in cylindrical container whose base has a diameter of 14 cm and height 20 cm. Company places a label around the surface of the container (as shown in the figure). If the label is placed 2 cm from top and bottom, What is the area of label.
View SolutionA bus stop is barricaded from the remaining part of the road, by using 50 hollow cones made of recycled cardboard. Each cone has a base diameter of 40 cm and height 1 m. If the outer side of each of the cones is to be painted and the cost of painting is 12 per m2 , what will be the cost of painting all these cones? (Use π = 3.14 and take √ 1.04 = 1.02)
View SolutionA solid toy is in the form of a hemisphere surmounted by a right circular cone. The height of the cone is 2 cm and the diameter of the base is 4 cm. Determine the volume of the toy. If a right circular cylinder circumscribes the toy, find the difference of the volumes of the cylinder and the toy.
View SolutionA toy is in the form of a hemisphere surmounted by a right circular cone of the same base radius as that of the hemisphere. If the radius of the base of the cone is 21cm and its volume is 2/3 of the volume of the hemisphere, calculate the height of the cone and the surface area of the toy. (Useπ=227).
View Solution
