The base of triangle T is 40 percent less than the length os rectangle R. The height T is 50 percent greater than the width of rectangle R. The area of triangle T is what percent of the area of rectangle R?
10
45
90
110
The correct Answer is:B
To solve the problem, we need to find the area of triangle T as a percentage of the area of rectangle R. Let's break it down step by step.
Step 1: Define Variables
Let the length of rectangle R be L and the width of rectangle R be W.
Step 2: Calculate the Base of Triangle T
The base of triangle T is 40% less than the length of rectangle R. Therefore, we can express the base B of triangle T as:
B=L−0.4L=0.6L
Step 3: Calculate the Height of Triangle T
The height of triangle T is 50% greater than the width of rectangle R. Thus, we can express the height H of triangle T as:
H=W+0.5W=1.5W
Step 4: Calculate the Area of Triangle T
The area AT of triangle T can be calculated using the formula for the area of a triangle:
AT=12×Base×Height=12×B×H
Substituting the values of B and H:
AT=12×(0.6L)×(1.5W)=12×0.6×1.5×L×W
Calculating the constants:
AT=12×0.9×L×W=0.45LW
Step 5: Calculate the Area of Rectangle R
The area AR of rectangle R is given by:
AR=L×W
Step 6: Calculate the Percentage of the Area of Triangle T to Rectangle R
To find what percent the area of triangle T is of the area of rectangle R, we use the formula:
Percentage=(ATAR)×100
Substituting the areas:
Percentage=(0.45LWLW)×100=0.45×100=45%
Final Answer
The area of triangle T is 45% of the area of rectangle R.
---
Let the length of rectangle R be L and the width of rectangle R be W.
The base of triangle T is 40% less than the length of rectangle R. Therefore, we can express the base B of triangle T as:
B=L−0.4L=0.6L
The height of triangle T is 50% greater than the width of rectangle R. Thus, we can express the height H of triangle T as:
H=W+0.5W=1.5W
The area AT of triangle T can be calculated using the formula for the area of a triangle:
AT=12×Base×Height=12×B×H
Substituting the values of B and H:
AT=12×(0.6L)×(1.5W)=12×0.6×1.5×L×W
Calculating the constants:
AT=12×0.9×L×W=0.45LW
The area AR of rectangle R is given by:
AR=L×W
To find what percent the area of triangle T is of the area of rectangle R, we use the formula:
Percentage=(ATAR)×100
Substituting the areas:
Percentage=(0.45LWLW)×100=0.45×100=45%
The area of triangle T is 45% of the area of rectangle R.
Topper's Solved these Questions
- BOOK - PRINCETONCHAPTER - GEOMETRYEXERCISE - Geometry Drill 2: Calculator-Permitted Section8videos
GEOMETRY
- BOOK - PRINCETONCHAPTER - GEOMETRYEXERCISE - EXAMPLES13videos
GEOMETRY
- BOOK - PRINCETONCHAPTER - FUNCTIONS AND GRAPHSEXERCISE - Functions and Graphs Drill 2: Calculator -Permitted Section6videos
FUNCTIONS AND GRAPHS
- BOOK - PRINCETONCHAPTER - GRID-INSEXERCISE - Grid-In Drill 2: Calculator-Permitted Section6videos
GRID-INS
Similar Questions
Each of equal sides of an isosceles triangle is 4 cm greater than its height. If the base of the triangle is 24 cm, calculate the perimeter and the area of the triangle.
View SolutionEach of equal sides of an isosceles triangles is 4 cm greater than its height. It the base of the triangle is 24 cm. Calculate the perimeter and the area of the triangle.
View Solution
Knowledge Check
- Question 1 - Select One
In the figure, ABCD is a rectangle, and the area of ΔACE is 10. What is the area of the rectangle?
 A18B22.5C36D44
A18B22.5C36D44 - Question 2 - Select One
The ratio of a side of square X to the length of rectangle Z is 3:4 . The ratio of a side of square X to the width of rectangle Z is 3:2. What is the ratio of the area of square X to the area of rectangle Z ?
A1:1B2:1C3:2D9:8 - Question 3 - Select One
The length of a certain rectangle is twice the width. If the area of the rectangle is 128, what is the length of the rectangle.
A4B8C16D2113
The length and the breadth of a rectangle are 6 cm and 4 cm respectively. Find the height of a triangle whose base is 6 cm and area is 3 times that of the rectangle.
View SolutionTo find the area of rectangle ABCD, note that the diagonal form a (5−12−13) right triangle so the width of the rectangle is 5. Hence,Find area of triangle.:
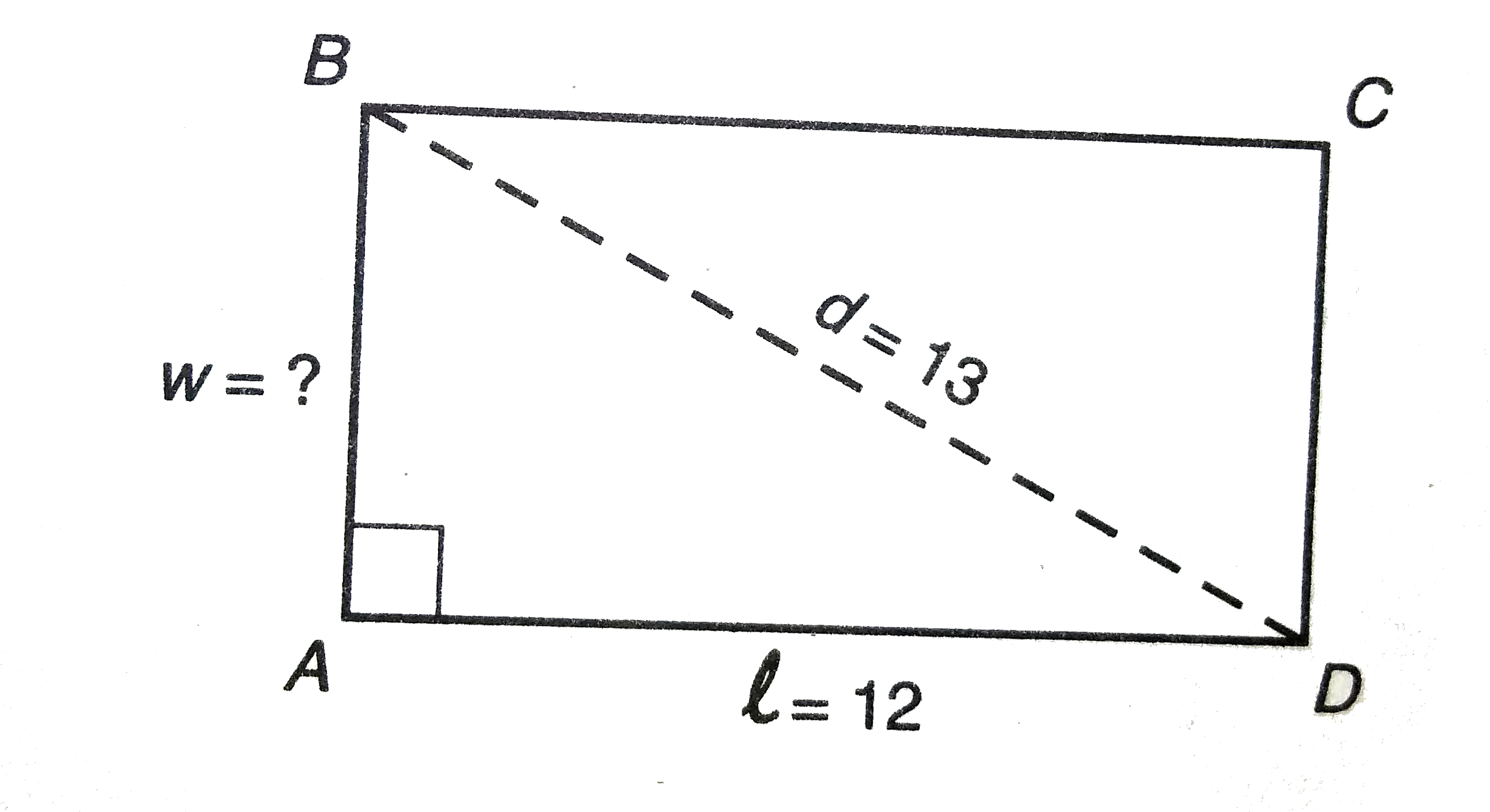 View Solution
View SolutionIn the figure, the area of rectangle EFGH is 3 units greater than the area of rectangle ABCD. What is the value of ab if a+b=8 ?
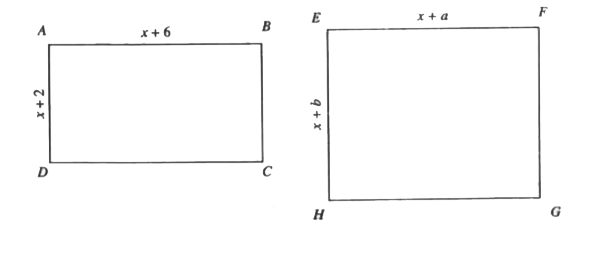 View Solution
View SolutionThe average length of all the sides of a rectangle equals twice the width of the rectangle. If the area of the rectangle is 18, what is its perimeter?
View SolutionThe length of a rectangle is 2 ft shorter than twice the width . Which of the following graphs represents the area of the rectangle in terms of its width ?
View Solution

