Nails are sold in 8-ounces and 20-ounce boxes. If 50 boxes of nails were sold and the total weight of the nails sold was less than 600 ounces, what is the greatest possible number of 20-ounce boxes that could have been sold?
33
25
17
16
The correct Answer is:D
To solve the problem step by step, we will define our variables, set up the inequalities based on the information provided, and then solve for the maximum number of 20-ounce boxes.
Step 1: Define Variables
Let:
- x = number of 8-ounce boxes sold
- y = number of 20-ounce boxes sold
Step 2: Set Up the Equations
From the problem, we know two things:
1. The total number of boxes sold is 50:
x+y=50
2. The total weight of the nails sold is less than 600 ounces:
8x+20y<600
Step 3: Express x in Terms of y
From the first equation, we can express x in terms of y:
x=50−y
Step 4: Substitute x in the Weight Inequality
Now, we substitute x in the weight inequality:
8(50−y)+20y<600
Expanding this gives:
400−8y+20y<600
Combining like terms results in:
400+12y<600
Step 5: Solve for y
Next, we isolate y:
12y<600−400
12y<200
Dividing both sides by 12 gives:
y<20012
Simplifying this fraction:
y<503≈16.67
Step 6: Determine the Greatest Integer Value for y
Since y must be an integer, the greatest possible value for y that satisfies this inequality is:
y≤16
Conclusion
Thus, the greatest possible number of 20-ounce boxes that could have been sold is:
16
Let:
- x = number of 8-ounce boxes sold
- y = number of 20-ounce boxes sold
From the problem, we know two things:
1. The total number of boxes sold is 50:
x+y=50
2. The total weight of the nails sold is less than 600 ounces:
8x+20y<600
From the first equation, we can express x in terms of y:
x=50−y
Now, we substitute x in the weight inequality:
8(50−y)+20y<600
Expanding this gives:
400−8y+20y<600
Combining like terms results in:
400+12y<600
Next, we isolate y:
12y<600−400
12y<200
Dividing both sides by 12 gives:
y<20012
Simplifying this fraction:
y<503≈16.67
Since y must be an integer, the greatest possible value for y that satisfies this inequality is:
y≤16
Thus, the greatest possible number of 20-ounce boxes that could have been sold is:
16
Topper's Solved these Questions
- BOOK - PRINCETONCHAPTER - OTHER ALGEBRA STRATEGIESEXERCISE - Algebra Strategies Drill 1: No Calculator Section4videos
OTHER ALGEBRA STRATEGIES
- BOOK - PRINCETONCHAPTER - MATH TEST 01EXERCISE - MCQs60videos
MATH TEST 01
- BOOK - PRINCETONCHAPTER - PRACTICE SECTION 2 EXERCISE - MCQs60videos
PRACTICE SECTION 2
Similar Questions
The length of a certain rectangle is twice the width. If the area of the rectangle is 128, what is the length of the rectangle.
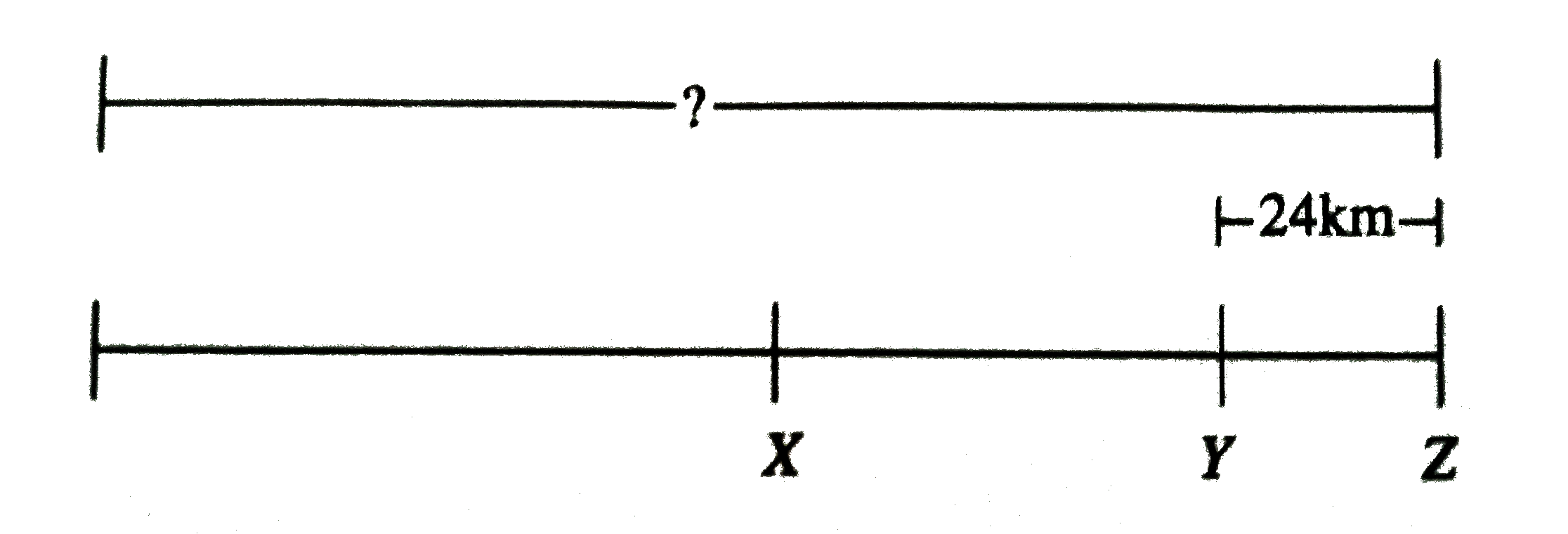
10:03View SolutionIn the hiking trail shown below .X marks the trail's halfway point .If ¯¯¯¯¯¯YZ measures 24 kilometers and is 13 the length of ¯¯¯¯xz , what is the total length , in kilometers of the trail ?
 01:19View Solution
01:19View SolutionWhich of the following expressions is equivalent to 2a+4b+6c ?
02:01View Solution66 once tilhen can be O 16 ounce La ller The Ounce 40 minu We Co bo
02:55View SolutionA carton contains 40 boxes of nails and each box weight 334kg. How much would a cartoon of nails weight?
02:31View SolutionThe postal rate for first-class mail is 44 cents for the first ounce or portion thereof and 17 cents for each additional ounce or portion thereof up to 3.5 ounces. The cost of a 3.5-ounce letter is 95cancel c. A formula for the cost in cents of first-class postage for a letter weighing N ounces (N≤3.5) is
02:26View SolutionIn 1854, during the California gold rush, each ounce of gold was worth $20, and the largest known mass of gold found in California was worth $62,400 in that year. What was the weight, in pounds, of this mass of gold? (16 ounces = 1 pound)
03:51View Solution1 जूल कितने अर्ग के बराबर होता है?
02:11View SolutionIf a 3-pound pizza is sliced in half and each half is sliced into thirds, what is the weight, in ounces, of each of the slices? (1 pound = 16 ounces)
03:50View SolutionIf 40 gumballs were weighed on a balancing scale, the gumballs would weigh approximately 1218 ounces. At the rate, what is the approximately number of gumballs it would take to weigh 36 ounces on the balancing scale?
02:33View SolutionA chef trimmed fat off a steak and was left with a steak weighing 8.80 ounces. If the weight of the fat was equal to 12 percent of the original weight, what was the original weight , in ounces, of the steak?
04:26View SolutionCarina has 100 ounces of coffee divided into 5 - and 10 - ounce packages. If she has 2 more 5 - ounce packages than 10 - ounce packeages, how many 10 - ounce packages does she have?
04:14View SolutionJoseph bought two varieties of rice, costing 5 cents per ounce and 6 cents per ounce each, and mixed them in some ratio. Then he sold the mixture at 7 cents per ounce, making a profit of 20 percent. What was the ratio of the mixture?
02:02View SolutionHow many ounces of a solution that is 30 percent salt must be added to a 50-ounce solution that is 10 percent salt so that the resulting solution is 20 percent salt?
01:25View SolutionColumn A1 Pound = 16 OuncesColumnBWeight of 16,000 ounces of riceWeight of 1,000 pounds of coal
03:01View Solution

