In a certain triangle, the measures of ∠Aand∠B are (6k−8)∘and(7k−45)∘, respectively. If sin∠Acos∠B=1, what is the value of k ?
The correct Answer is:11
To solve the problem step by step, we will follow the logic presented in the video transcript.
Step 1: Set up the equation
We are given that:
- ∠A=6k−8
- ∠B=7k−45
The condition provided is:
sin∠Acos∠B=1
This implies:
sin∠A=cos∠B
Step 2: Use the trigonometric identity
From the identity sinx=cosy, we know that:
sinx=cosyif and only ifx=90∘−yory=90∘−x
Thus, we can write:
6k−8=90−(7k−45)
Step 3: Simplify the equation
Now, simplify the right side:
6k−8=90−7k+45
Combine like terms:
6k−8=135−7k
Step 4: Rearrange the equation
Now, we will bring all terms involving k to one side and constant terms to the other side:
6k+7k=135+8
This simplifies to:
13k=143
Step 5: Solve for k
Now, divide both sides by 13:
k=14313
Calculating this gives:
k=11
Final Answer
Thus, the value of k is:
11
We are given that:
- ∠A=6k−8
- ∠B=7k−45
sin∠Acos∠B=1
This implies:
sin∠A=cos∠B
From the identity sinx=cosy, we know that:
sinx=cosyif and only ifx=90∘−yory=90∘−x
Thus, we can write:
6k−8=90−(7k−45)
Now, simplify the right side:
6k−8=90−7k+45
Combine like terms:
6k−8=135−7k
Now, we will bring all terms involving k to one side and constant terms to the other side:
6k+7k=135+8
This simplifies to:
13k=143
Now, divide both sides by 13:
k=14313
Calculating this gives:
k=11
Thus, the value of k is:
11
Topper's Solved these Questions
- TRIGONOMETRY Book:KAPLANChapter:TRIGONOMETRY Exercise:SINE, COSINE, AND TANGENT
Explore 1 Video
- TRIGONOMETRY Book:KAPLANChapter:TRIGONOMETRY Exercise:SINE, COSINE, AND TANGENT
Explore 1 Video
- THE MATHOD OF SAT MATH QUESTIONS Book:KAPLANChapter:THE MATHOD OF SAT MATH QUESTIONS Exercise:TRY ON YOUR OWN
Explore 10 Videos
Similar Questions
Knowledge Check
In this triangle, what is the degree measure of angle c ?
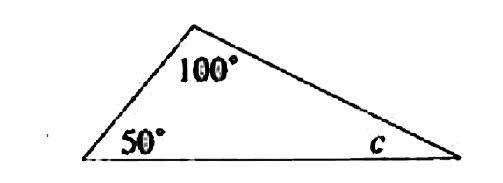 A17B20C30D40
A17B20C30D40The two angles of triangle measure 63∘ and 47∘ respectively. Find the measure of the the third angle of the triangle.
A80∘B70∘C90∘D100∘In triangles ABC, the measures of angles a, b, and c, respectively, are in the ratio 2:3:4.What is the measure of angle b?
A20B40C60D80
If in a ΔABC,∠A=45∘,∠B=75∘, then
View SolutionIf a vertex, the circumcenter, and the centroid of a triangle are (0, 0), (3,4), and (6, 8), respectively, then the triangle must be (a) a right-angled triangle (b) an equilateral triangle (c) an isosceles triangle (d) a right-angled isosceles triangle
View SolutionThe position vectors of vertices of △ABC are (1,−2),(−7,6)and(115,25) respectively. The measure of the interior angle A of the △ABC, is,
View SolutionIn a triangle ABC,sinA−cosB=CosC, then angle B is
View SolutionIn a certain isosceles triangle , the measure of the vertex angle is four times the measure of each of the base angles , what is the measure , in degrees, of the vertex angle ?
View Solution
