Triangle DEF is similar to triangle ABC, and both are plotted on a coordinate plane (not shown). The vertices of triange DEF are D(3,2),E(3,−1),andF(−1,−1). Two of triangle ABC's vettices are quadrant of the coordinate plane as vertex D, what is the y-coordinate of vertex A ?
The correct Answer is:9
To solve the problem, we need to find the y-coordinate of vertex A of triangle ABC, given that triangle DEF is similar to triangle ABC and the coordinates of the vertices of triangle DEF are D(3, 2), E(3, -1), and F(-1, -1).
1. Identify the Coordinates of Triangle DEF:
- The vertices of triangle DEF are given as:
- D(3, 2)
- E(3, -1)
- F(-1, -1)
2. Determine the Length of Side FE:
- Calculate the distance between points F and E:
- F(-1, -1) to E(3, -1)
- The length of FE = |x-coordinate of E - x-coordinate of F| = |3 - (-1)| = |3 + 1| = 4 units.
3. Identify the Coordinates of Triangle ABC:
- Two vertices of triangle ABC are given as:
- B(-8, -3)
- C(8, -3)
- Since both points B and C share the same y-coordinate (-3), they lie on the same horizontal line.
4. Determine the Length of Side BC:
- Calculate the distance between points B and C:
- B(-8, -3) to C(8, -3)
- The length of BC = |x-coordinate of C - x-coordinate of B| = |8 - (-8)| = |8 + 8| = 16 units.
5. Establish the Ratio of Similarity:
- Since triangles DEF and ABC are similar, the ratio of corresponding sides must be equal.
- The ratio of sides FE to BC is:
- FE : BC = 4 : 16 = 1 : 4.
6. Determine the Length of Side DE:
- Calculate the distance between points D and E:
- D(3, 2) to E(3, -1)
- The length of DE = |y-coordinate of D - y-coordinate of E| = |2 - (-1)| = |2 + 1| = 3 units.
7. Calculate the Length of Side AC:
- Using the ratio established, we can find the length of side AC:
- DE : AC = 1 : 4
- If DE = 3, then AC = 3 * 4 = 12 units.
8. Determine the Y-coordinate of Vertex A:
- Since vertex A is directly above point C, we add the length of AC to the y-coordinate of point C:
- The y-coordinate of C is -3.
- Therefore, the y-coordinate of A = y-coordinate of C + length of AC = -3 + 12 = 9.
Final Answer:
The y-coordinate of vertex A is 9.
- The vertices of triangle DEF are given as:
- D(3, 2)
- E(3, -1)
- F(-1, -1)
- Calculate the distance between points F and E:
- F(-1, -1) to E(3, -1)
- The length of FE = |x-coordinate of E - x-coordinate of F| = |3 - (-1)| = |3 + 1| = 4 units.
- Two vertices of triangle ABC are given as:
- B(-8, -3)
- C(8, -3)
- Since both points B and C share the same y-coordinate (-3), they lie on the same horizontal line.
- Calculate the distance between points B and C:
- B(-8, -3) to C(8, -3)
- The length of BC = |x-coordinate of C - x-coordinate of B| = |8 - (-8)| = |8 + 8| = 16 units.
- Since triangles DEF and ABC are similar, the ratio of corresponding sides must be equal.
- The ratio of sides FE to BC is:
- FE : BC = 4 : 16 = 1 : 4.
- Calculate the distance between points D and E:
- D(3, 2) to E(3, -1)
- The length of DE = |y-coordinate of D - y-coordinate of E| = |2 - (-1)| = |2 + 1| = 3 units.
- Using the ratio established, we can find the length of side AC:
- DE : AC = 1 : 4
- If DE = 3, then AC = 3 * 4 = 12 units.
- Since vertex A is directly above point C, we add the length of AC to the y-coordinate of point C:
- The y-coordinate of C is -3.
- Therefore, the y-coordinate of A = y-coordinate of C + length of AC = -3 + 12 = 9.
The y-coordinate of vertex A is 9.
Topper's Solved these Questions
- GEOMETRY Book:KAPLANChapter:GEOMETRY Exercise:CIRCLES
Explore 1 Video
- GEOMETRY Book:KAPLANChapter:GEOMETRY Exercise:ARC LENGTH AND SECTORS
Explore 1 Video
- GEOMETRY Book:KAPLANChapter:GEOMETRY Exercise:THREE-DIMENSIONAL FIGURES
Explore 1 Video
- FUNCTIONS Book:KAPLANChapter:FUNCTIONS Exercise:DESCRIBING REAL-LIFE SITUATIONS WITH FUNCTIONS
Explore 1 Video
- IMAGINARY NUMBERS Book:KAPLANChapter:IMAGINARY NUMBERS Exercise:ARITHMETIC OPERATIONS WITH COMPLEX NUMBERS
Explore 1 Video
Similar Questions
Knowledge Check
For the rectangle shown in the standard ( x, y) Coordinate plane below , what are the coordinate of the unlabeled vertex ?
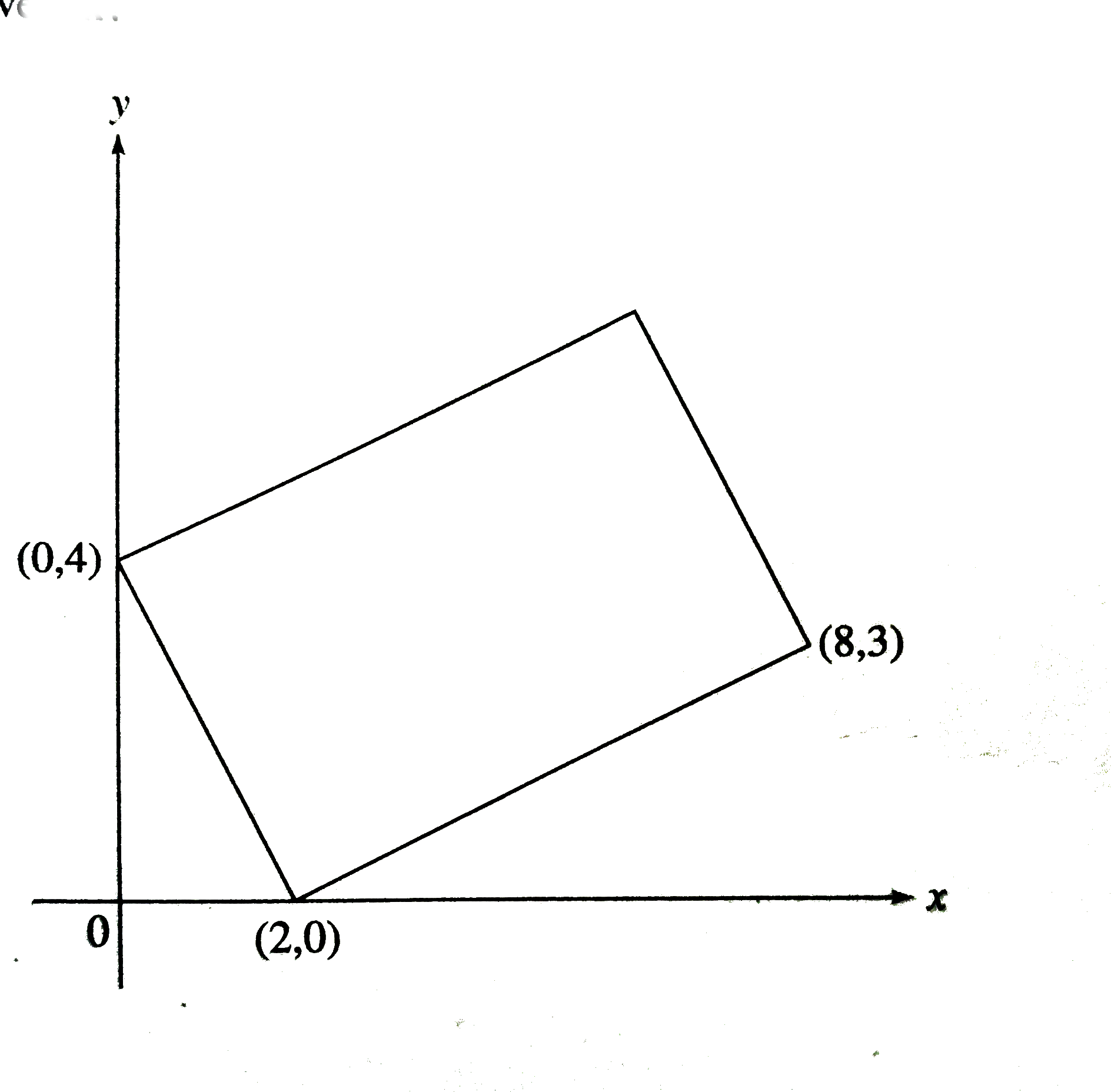 A(4,5)B(4,7)C(5,72)D(6,7)
A(4,5)B(4,7)C(5,72)D(6,7)
if the coordinates of the mid points of the Sides of a triangle are (1,2),(0,−1) and (2,−1).Find the coordinates of its vertices :
View SolutionFind the coordinates of the orthocentre of the triangle whose vertices are (0,1),(2,−1)and(−1,3)
View SolutionThe coordinates of the middle points of the sides of a triangle are (1,1),(2,3)and(4,1), find the coordinates of its vertices.
View SolutionTwo vertices of a triangle are (5,−1) and (−2,3) If the orthocentre of the triangle is the origin, find the coordinates of the third point.
View SolutionABC is an isosceles triangle. If the coordinates of the base are B(1, 3) and C(-2, 7). The coordinates of vertex A can be
View SolutionTwo vertices of a triangle are (3, 4, 2) and (1, 3, 3) If the medians of the triangle intersect at (0, 3,-1), then the coordinates of the third vertex of the triangle are
View SolutionFind the area of a triangle ABC if the coordinates of the middle points of the sides of the triangle are (−1,−2),(6,1)and(3,5)
View Solution