An object lauched upwards at an angle has parabolic motion. The height h, of a projectile at time t is given by the equation h=12at2+vyt+h0, where a is the acceleration due to gravity, vv is the vertical component of the velocity, and h0 is the initial height. Which of the following equations correctly represents the object's acceleration due to gravity in terms of the other variables ?
a=h−vvt−h0t
a=h−vvt−h02t2
a=2(h−vvt−h0)t2
a=t√2(h−vvt−h0)
The correct Answer is:C
Step by step video, text & image solution for An object lauched upwards at an angle has parabolic motion. The height h, of a projectile at time t is given by the equation h =1/2 at ^(2) + v _(y)t + h _(0), where a is the acceleration due to gravity, v _(v) is the vertical component of the velocity, and h _(0) is the initial height. Which of the following equations correctly represents the object's acceleration due to gravity in terms of the other variables ? by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSBOOK - KAPLANCHAPTER - EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSEXERCISE - EXPONENTS
1 Video
- EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSBOOK - KAPLANCHAPTER - EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSEXERCISE - POLYNOMIALS
1 Video
- EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSBOOK - KAPLANCHAPTER - EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSEXERCISE - RATIONAL EXPRESSIONS AND EQUATIONS
1 Video
- ANSWERING SAT READING QUESTIONS BOOK - KAPLANCHAPTER - ANSWERING SAT READING QUESTIONS EXERCISE - TRY ON YOUR OWN
22 Videos
- FUNCTIONS BOOK - KAPLANCHAPTER - FUNCTIONS EXERCISE - DESCRIBING REAL-LIFE SITUATIONS WITH FUNCTIONS
1 Video
Similar Questions
A particle is thrown vertically upwards with a velocity v. It returns to the ground in time T. which of the following graphs correctly represents the motion ?
View Solution
The approximate height h of an object launched vertically upward after an elapsed time t is represented by the equation h=12at2+vot+ho, where a is acceleration due to gravity, vo is the object's initial velocity, and ho is the objects initial height. the table aabove gives the acceleration due to gravity on Earth's moon and several planets. If two identical objects launched vertically upward at an initial velocity of 40m/s from the surfaces of Mars and Earth's moon approximately how many more seconds will it take for the moon projectile to return to the ground than the Mars projectile?
View Solution
Knowledge Check
The distance a free falling object has traveled can be modeled by the equation, d=12at2 where a is acceleration due to gravity and t is the amount of time the object has fallen. What is t in terms of a and d?
At=√da2Bt=√2daCt=(da2)2Dt=(3da)2A cylinder has volume V, height h, and base diameter d. Which of the following represents d in terms of V and h?
Ad=√VπhBd=√vπhCd=√2VπhDd=√4VπhThe velocity of a body which has fallen under gravity varies as gahb where g is the acceleration due to gravity at a place and h is the height through which the body has fallen, a and b are given by
Aa = 1, b = 1/2Ba = b = 1Ca = 1/2, b = 1Da = 1/2, b = 1/2
The graph shown the variation with times t of the velocity v of an object . Which one of the following graphs best represents the variation of acceleration a of the object with time t?
View SolutionThe position of a particle at time t is given by the equation x(t)=V0A(1−eAt)
V0 = constant and A > 0
Dimensions of V0 and A respectively are
View SolutionTotal mechanical energy E of an object of mass m, at a height h above the ground is given by the relation
E = mgh +p22m
Find the dimensions of p. (g = acceleration due to gravity).
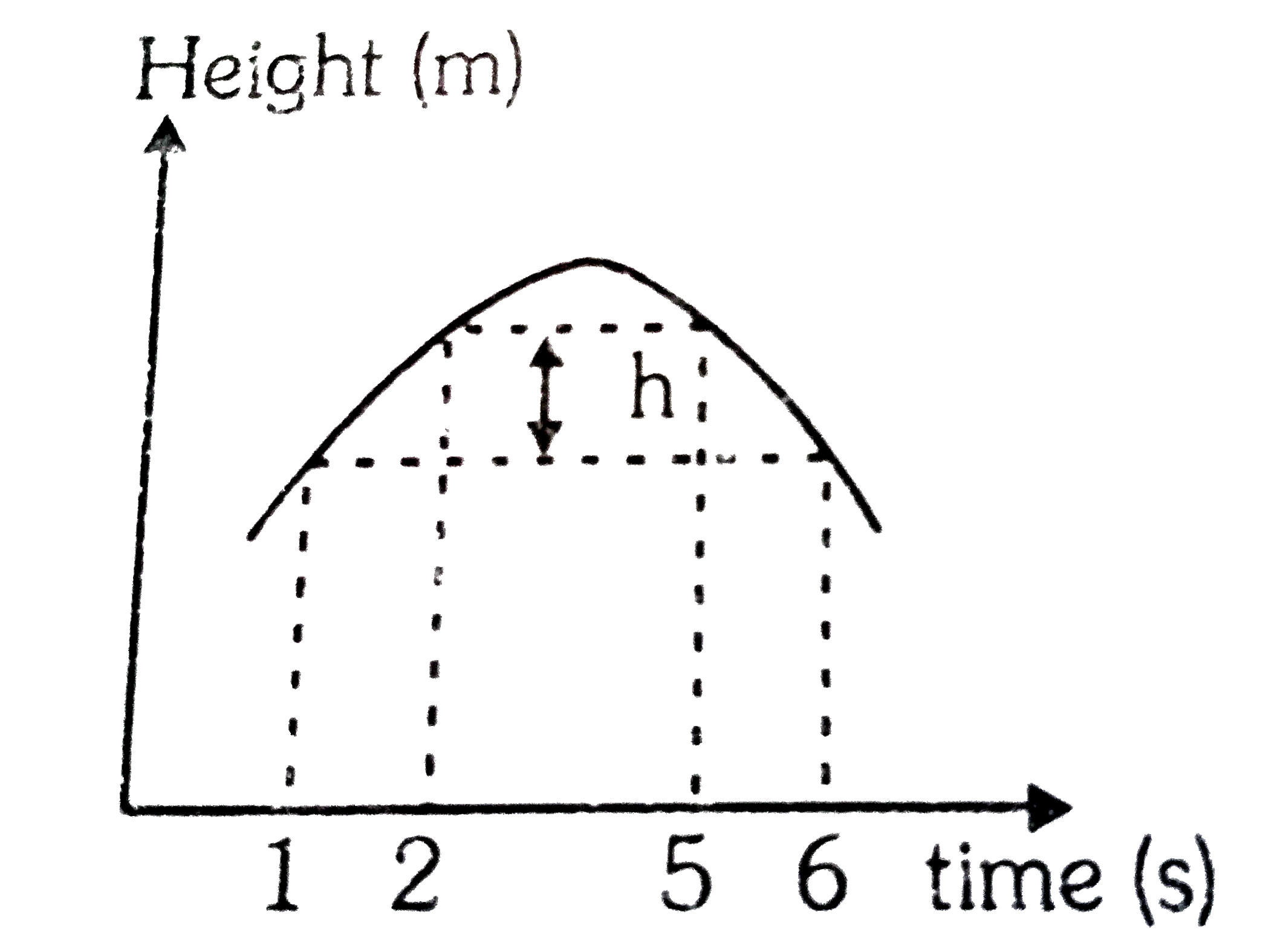
View SolutionA ball is thrown upwards . Its height varies with time as shown in figure. If the acceleration due to gravity is 7.5m/s2, then the height h is
View SolutionThe velocity of a freely falling body changes as gphqwhere g is acceleration due to gravity and h is the height. The values of p and q are
View Solution
