The function f is a parabolic function that intersects the x-axis. Which of the following statements must be true ?
The function has at least one real root.
The function has no real roots.
The function intersects the positive y axis.
The function has two zeros.
The correct Answer is:A
To determine which statements must be true for a parabolic function f that intersects the x-axis, let's analyze the properties of parabolas and the implications of intersecting the x-axis.
1. Understanding Parabolic Functions:
A parabolic function can be represented in the form f(x)=ax2+bx+c, where a≠0. The graph of this function is a parabola, which can open upwards (if a>0) or downwards (if a<0).
Hint: Remember that the direction of the parabola is determined by the coefficient a.
2. Intersection with the x-axis:
If a parabolic function intersects the x-axis, it means that there are values of x for which f(x)=0. These values are known as the roots or zeros of the function.
Hint: The points where the parabola crosses the x-axis correspond to the real roots of the equation f(x)=0.
3. Analyzing the Options:
- Option A: The function has at least one real root.
- Since the function intersects the x-axis, it must have at least one real root. This statement is true.
- Option B: The function has no real root.
- This statement contradicts the premise that the function intersects the x-axis. Therefore, this option is false.
- Option C: The function intersects the positive y-axis.
- A parabola can intersect the y-axis at any point, positive or negative. Therefore, this statement is not necessarily true for all parabolas.
- Option D: The function has two roots.
- A parabola can have two roots (intersecting the x-axis at two points), one root (touching the x-axis at one point), or no roots (not intersecting the x-axis). Since we know it intersects the x-axis, it can have either one or two roots. Thus, this statement is not necessarily true.
4. Conclusion:
The only statement that must be true for a parabolic function that intersects the x-axis is Option A: The function has at least one real root.
Final Answer: The correct statement is A: The function has at least one real root.
A parabolic function can be represented in the form f(x)=ax2+bx+c, where a≠0. The graph of this function is a parabola, which can open upwards (if a>0) or downwards (if a<0).
If a parabolic function intersects the x-axis, it means that there are values of x for which f(x)=0. These values are known as the roots or zeros of the function.
- Option A: The function has at least one real root.
- Since the function intersects the x-axis, it must have at least one real root. This statement is true.
- Option B: The function has no real root.
- This statement contradicts the premise that the function intersects the x-axis. Therefore, this option is false.
- Option C: The function intersects the positive y-axis.
- A parabola can intersect the y-axis at any point, positive or negative. Therefore, this statement is not necessarily true for all parabolas.
- Option D: The function has two roots.
- A parabola can have two roots (intersecting the x-axis at two points), one root (touching the x-axis at one point), or no roots (not intersecting the x-axis). Since we know it intersects the x-axis, it can have either one or two roots. Thus, this statement is not necessarily true.
The only statement that must be true for a parabolic function that intersects the x-axis is Option A: The function has at least one real root.
Topper's Solved these Questions
- EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSBOOK - KAPLANCHAPTER - EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSEXERCISE - TRY ON YOUR OWN
44 Videos
- EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSBOOK - KAPLANCHAPTER - EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSEXERCISE - EXPONENTS
1 Video
- ANSWERING SAT READING QUESTIONS BOOK - KAPLANCHAPTER - ANSWERING SAT READING QUESTIONS EXERCISE - TRY ON YOUR OWN
22 Videos
- FUNCTIONS BOOK - KAPLANCHAPTER - FUNCTIONS EXERCISE - DESCRIBING REAL-LIFE SITUATIONS WITH FUNCTIONS
1 Video
Similar Questions
Figure shows a plot of the potential energy as a function of x for a particle moving along the x-axis. Which of the following statement(s) is/are true?
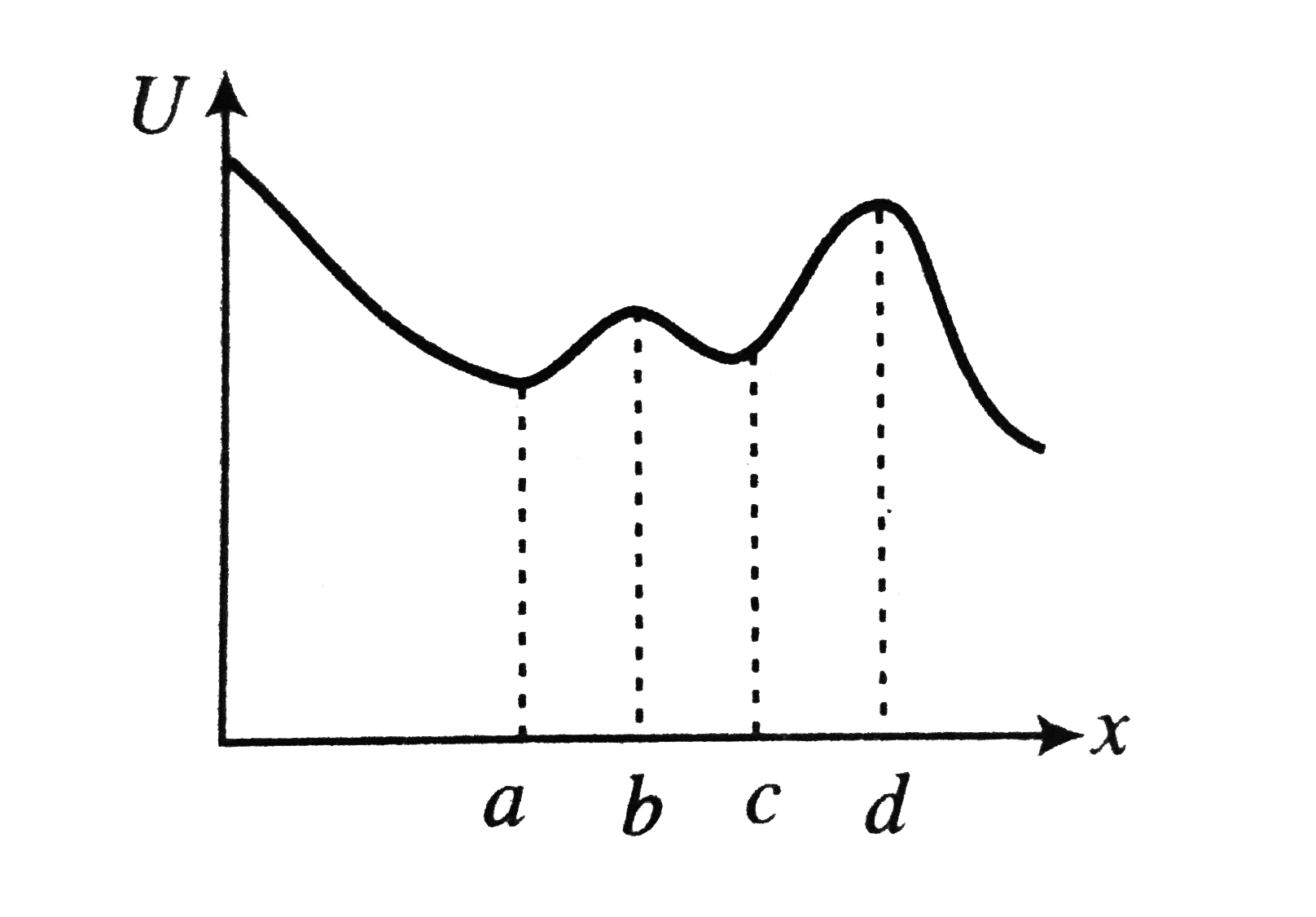
View SolutionFigure shows a plot of the potential energy as a function of x for a particle moving along the x-axis. Which of the following statement(s) is/are true?

View Solution
Knowledge Check
If f(x)=x3, which of the following must be true ?
Af(−x)=f(x)Bf(−x)=−f(−x)Cf(−x)=−f(x)Df(x)=−f(x)A function is said to be even if f(x)=f(-x). Which of the following is not an even function?
Ay=|x|By=secxCy=logx2Dy=x2+sinx
For function f(x)=lnxx, which of the following statements are true?
View SolutionLet f(x)=g(x)h(x), where g and h are continuous functions on the open interval (a, b). Which of the following statements is true for a<x<b ?
View SolutionA function f is defined on an interval [a, b]. Which of the following statement(s) is are incorrect? (A) If f(a) and f(b) have opposite signs,then there must be a point c∈(a,b) such that f(c)=0.
View SolutionFor a function f:A→B such that n(A)=a,n(B)=b(a,b∈N) then which of the following statements must be CORRECT?
View SolutionThe function f(x)=x6−x−1 cuts the x-axis
View SolutionLet f(x)=sgn(cot−1x)+tan(π2[x]), where [x] is the greatest integer function less than or equal to x, then which of the following alternatives is/are true? f(x) is many-one but not an even function. f(x) is a periodic function. f(x) is a bounded function. The graph of f(x) remains above the x-axis.
View Solution
