A tube A of radius r is connected to two other tubes B and C with the help of a junction valve. The tubes B and C have radii r2 and r3 and the flow velocity in each is v and 3v respectively. If the flow velocity in tube A is nmv, when n and m are integers, then what is the value of n+m ?
The correct Answer is:19
To solve the problem, we will apply the principle of conservation of mass, which states that the mass flow rate must be constant in a closed system. This can be expressed using the equation of continuity for incompressible fluids:
A1v1=A2v2+A3v3
Where:
- A1 is the cross-sectional area of tube A
- v1 is the flow velocity in tube A
- A2 is the cross-sectional area of tube B
- v2 is the flow velocity in tube B
- A3 is the cross-sectional area of tube C
- v3 is the flow velocity in tube C
Step 1: Calculate the cross-sectional areas
The cross-sectional area A of a tube is given by the formula:
A=πr2
- For tube A (radius r):
A1=πr2
- For tube B (radius r2):
A2=π(r2)2=πr24
- For tube C (radius r3):
A3=π(r3)2=πr29
Step 2: Substitute the areas and velocities into the continuity equation
Given that the flow velocity in tube B is v and in tube C is 3v, we can substitute these values into the continuity equation:
A1v1=A2v+A3(3v)
Substituting the areas we calculated:
πr2v1=(πr24)v+(πr29)(3v)
Step 3: Simplify the equation
We can cancel π from both sides:
r2v1=r24v+3r29v
Now, simplifying the right-hand side:
r2v1=r24v+13r2v
Finding a common denominator (which is 12):
r2v1=(312+412)r2v
r2v1=712r2v
Step 4: Solve for v1
Now we can divide both sides by r2:
v1=712v
Step 5: Identify n and m
From the expression v1=nmv, we can see that n=7 and m=12.
Step 6: Calculate n+m
Thus, the value of n+m is:
n+m=7+12=19
Final Answer
The final answer is 19.
---
- A1 is the cross-sectional area of tube A
- v1 is the flow velocity in tube A
- A2 is the cross-sectional area of tube B
- v2 is the flow velocity in tube B
- A3 is the cross-sectional area of tube C
- v3 is the flow velocity in tube C
The cross-sectional area A of a tube is given by the formula:
A1=πr2
A2=π(r2)2=πr24
A3=π(r3)2=πr29
Given that the flow velocity in tube B is v and in tube C is 3v, we can substitute these values into the continuity equation:
We can cancel π from both sides:
Now we can divide both sides by r2:
From the expression v1=nmv, we can see that n=7 and m=12.
Thus, the value of n+m is:
The final answer is 19.
Topper's Solved these Questions
Similar Questions
Two capillaries of small cross section are connected as shown in the figure. The right tube has cross sectional radius R and left one has a radius of r(<R). The tube of radius R is very long where as the tube of radius r is of short length. Water is slowly poured in the right tube. Contact angle for the tube wall and water is θ=0∘. Let h be the height difference between water surface in the right and left tube. Surface tension of water is T and its density is ρ.
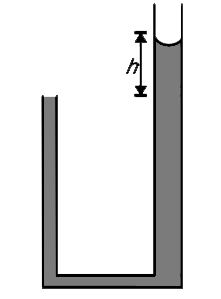
(a) Find the value of h if the water surface in the left tube is found to be flat.
(b) Find the maximum value of h for which water will not flow out of the left tube .
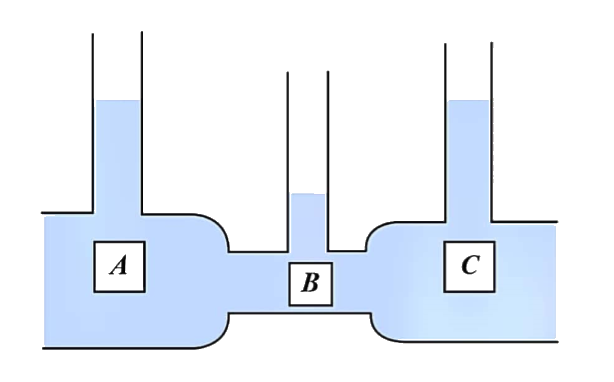
View SolutionA non-viscous liquid is flowing through a horizontal pipe as shown in the figure. Three tube A,B and C are connected to the pipe. The radii of the tubes A, B and C at the junction are 2 cm, 1 cm and 2 cm respectively. It can be said that the
View Solution
Knowledge Check
Two planets of masses M and M2 have radii R and R2 respectively. If ratio of escape velocities from their surfaces v1v2 is n4 , then find n :
A3B1C2D4In the figure, an ideal liquid flows through the tube, which is of uniform cross section. The liquid has velocities vA and vB, and pressures PA and PB at the points A and B, respectively. Then
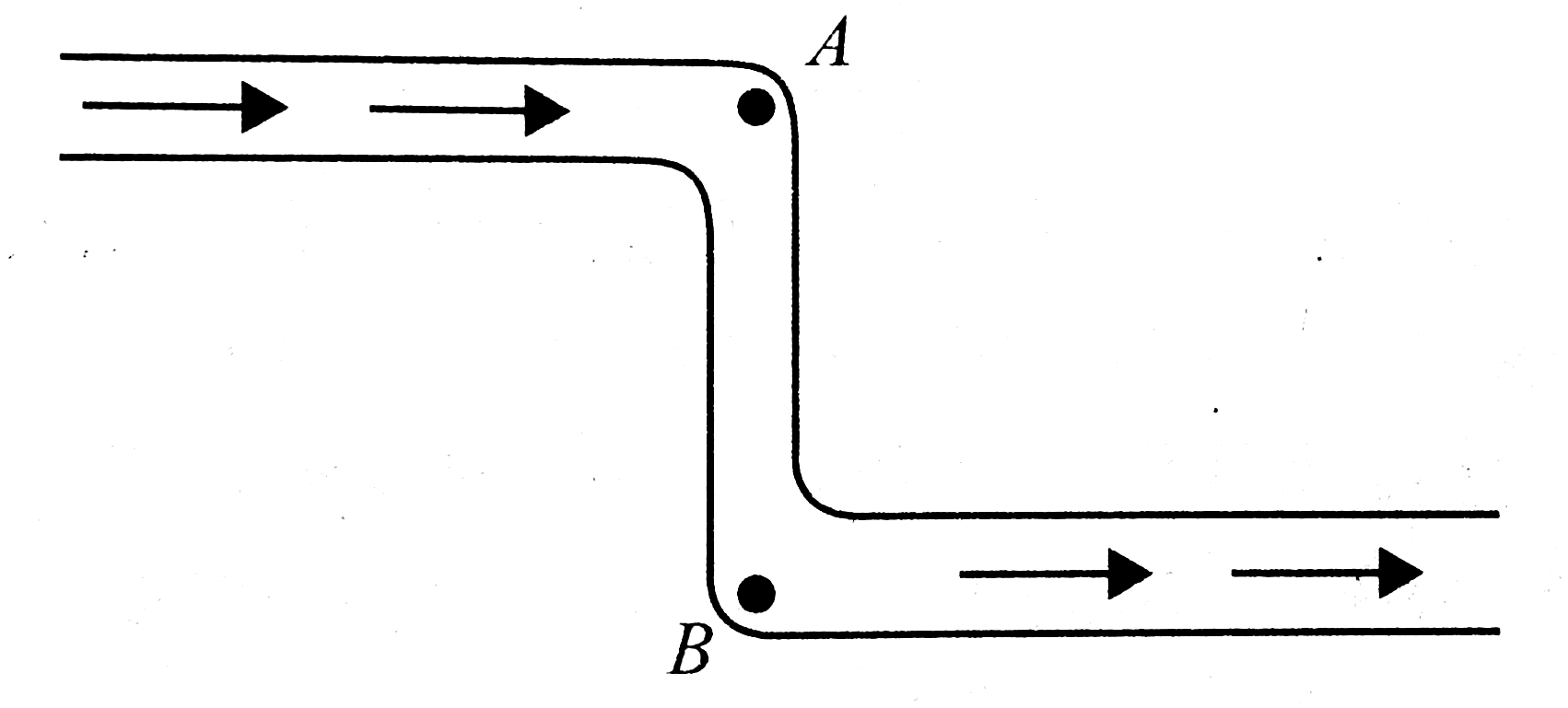 AvA=vBBvA>vBCPA=PBDPB>PA
AvA=vBBvA>vBCPA=PBDPB>PATwo masses m, and m, moving with velocities vaandvb in opposite direction collide elastically and after the collision maandmb move with velocities vbandva respectively. Then the ratio mamb is
A(va−vbva+vb)Bva+vbva+vbC1D12
Two tubes A and B are in series. The radius of A is R and that of B is 2R. If water flows through A with velocity v then the velocity of water through B is
View SolutionWater is flowing through a tube of radius r with a speed v. If this tube is joined to another tube of radius r/2, what is the speed of water in the second tube?
View SolutionAn idel fluid is flowing in a tube of varying corss- section .At some point the radius of the tube is r and the velocity of flow is v .The velocity of flow at another point, where the radius is r/2 is :
View SolutionIf the orbital velocity of a planet is given by v=GaMbRc then
View SolutionThe r.m.s velocity of the molecules of a gas is C and velocity of sound in the gas is V. The relation between V and C is
View Solution

