The molar heat capacity in a process of a diatomic gas if it does a work of Q4 when a heat of Q is supplied to it is
A
25R
B
52R
C
103R
D
67R
Video Solution
Text Solution
The correct Answer is:c
dU=CvdT=(52R)dT
⇒dT=2(dU)5R
From first law of thermodynamics, dU=dQ=dW
or dU=Q−Q4=3Q4
Now, molar heat capacity.
C=dQdT=Q2(dU5R)=5QR2(3Q4)=103R
|
Topper's Solved these Questions
- LAWS OF THERMODYNAMICSBook:BITSAT GUIDEChapter:LAWS OF THERMODYNAMICSExercise:6
Explore 2 Videos
- LAWS OF THERMODYNAMICSBook:BITSAT GUIDEChapter:LAWS OF THERMODYNAMICSExercise:7
Explore 2 Videos
- LAWS OF THERMODYNAMICSBook:BITSAT GUIDEChapter:LAWS OF THERMODYNAMICSExercise:4
Explore 2 Videos
- HEAT, TEMPERATURE AND CALORIMETRYBook:BITSAT GUIDEChapter:HEAT, TEMPERATURE AND CALORIMETRYExercise:Bitsat archives
Explore 9 Videos
- MAGNETOSTATICS Book:BITSAT GUIDEChapter:MAGNETOSTATICS Exercise:BITSAT Archives
Explore 8 Videos
Similar Questions
Knowledge Check
The molar heat capacity of a gas in a process
Ais either CVorCPBlies between CVorCPCmay range from zero to infinityDcan have any real valueMolar heat capacity of a gas is
AExtensive propertyBIntensive propertyCChemical property of gasDColligative propertyThe molar heat capacity for the process shown in fig. is
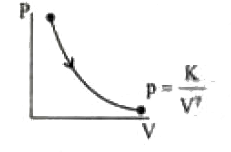 AC=CpBC=CvCC>CvDC=0
AC=CpBC=CvCC>CvDC=0
The heat capacity of a diatomic gas is higher than that of a monatomic gas.
View SolutionMolar heat capacity of a gas at constant volume.
View SolutionThe molar heat capacity for the process shown in fig. is
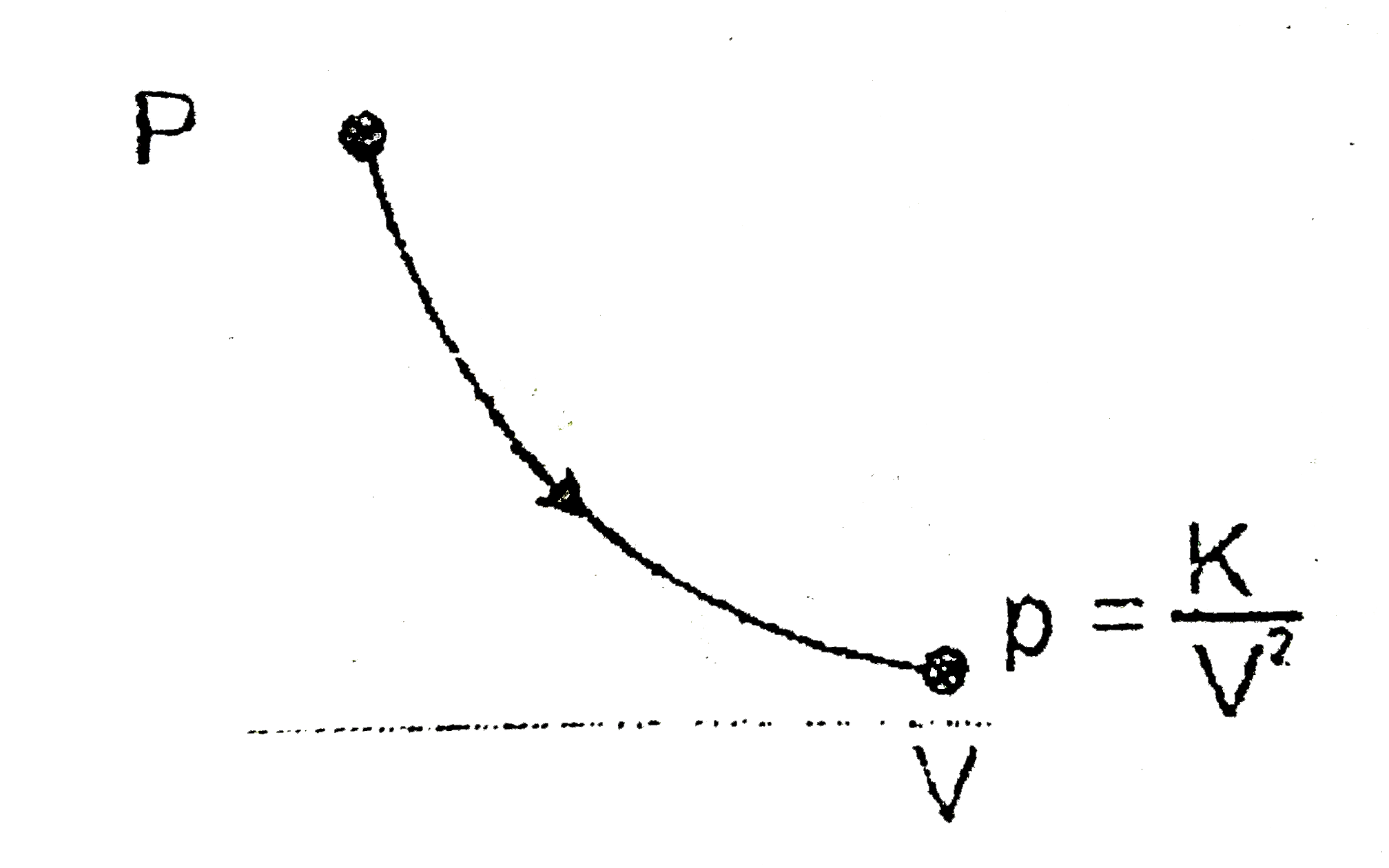
View SolutionThe molar heat capacity for the process shown in figure is
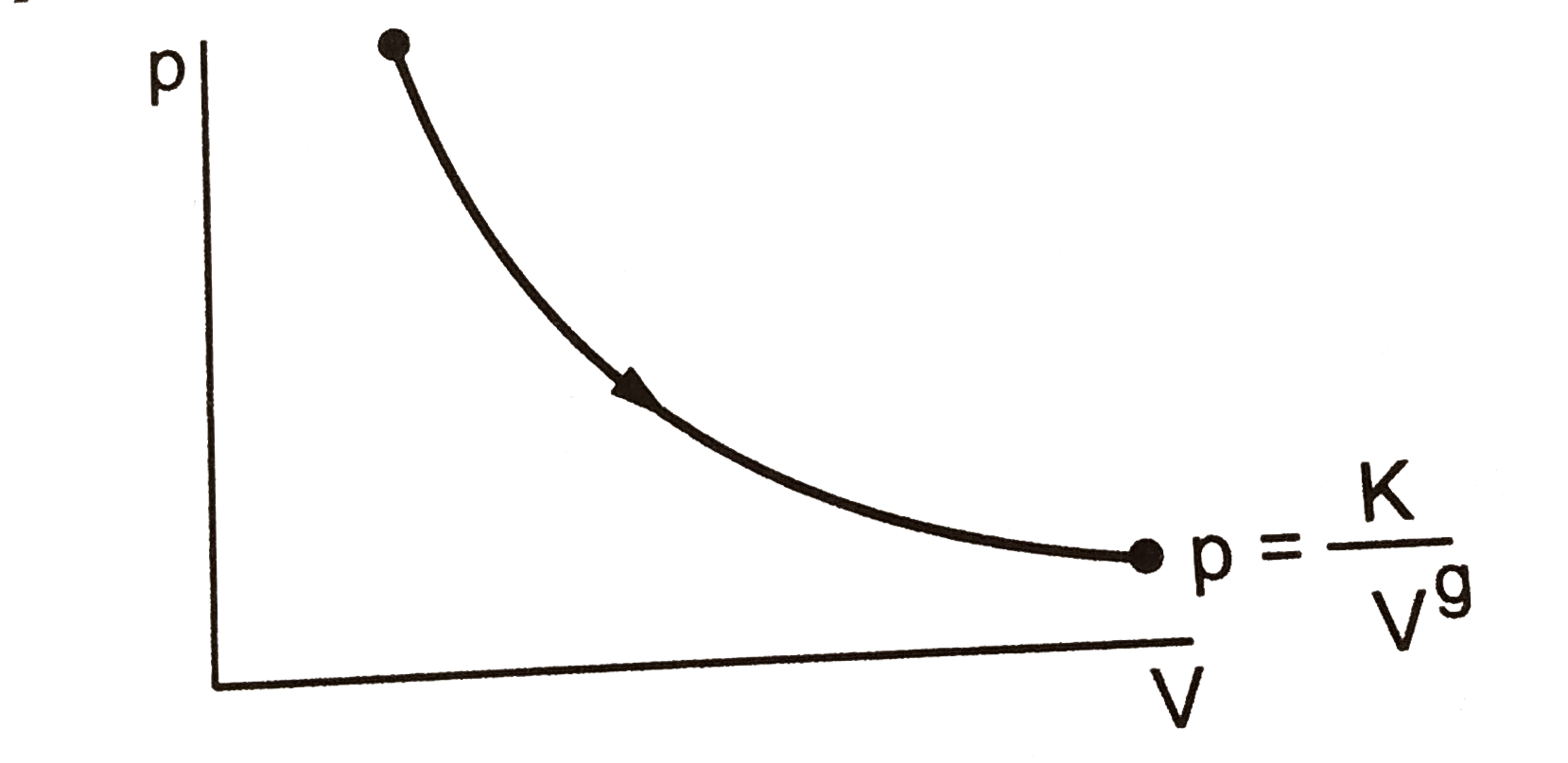
View SolutionIn a process, the molar heat capacity of a diatomic gas is 103R. When heat Q is supplied to the gas, find the work done by the gas
View Solution

