There is a shell of mass M and density of shell is uniform. The work done to take a point mass from point A to B is (AB=r)

GmMr
GmMR
−GmMr
zero
The correct Answer is:D
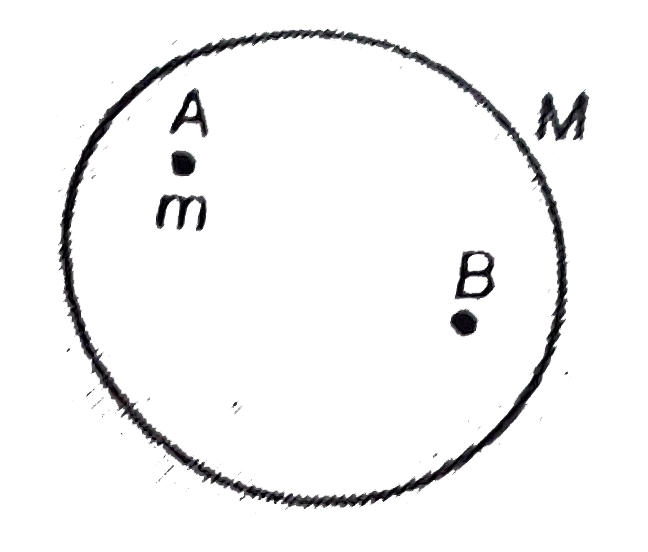
The gravitational field at A and B are zero. So, no work required to make change between the points A and B.
Topper's Solved these Questions
- GRAVITATIONBook:BITSAT GUIDEChapter:GRAVITATIONExercise:BITSAT Archives
Explore 15 Videos
- ELASTICITYBook:BITSAT GUIDEChapter:ELASTICITYExercise:BITSAT ARCHIVES
Explore 9 Videos
- HEAT, TEMPERATURE AND CALORIMETRYBook:BITSAT GUIDEChapter:HEAT, TEMPERATURE AND CALORIMETRYExercise:Bitsat archives
Explore 9 Videos
Similar Questions
A mass of 50 kg is placed at the centre of a uniform spherical shell of mass 100 kg and radius 50 m. If the gravitational potential at a point, 25 m from the centre is V kg/m. The value of V is:
View SolutionA thin spherical shell of total mass M and radius R is held fixed. There is a small hole in the shell. A mass m is released from rest a distance R from the hole along a line that passes through the hole and also through the centre of the shell. This mass subsequently moves under the gravitational force of the shell. How long does the mass take to travel from the hole to the point diametrically opposite.
View Solution
Knowledge Check
A thin uniform disc (see figure) of mass M has outer radius 4R and inner radius 3R. The work required to take a unit mass for point P on its axis to infinity is
 A2GM7R(4√2−5)B−2GM7R(4√−5)CGM4RD2GM5R(√2−1)
A2GM7R(4√2−5)B−2GM7R(4√−5)CGM4RD2GM5R(√2−1)A ring has a total mass M but non-uniformly distributed over its circumference. The radius of the ring is R. A point mass m is placed at the centre of the ring. Workdone in taking away this point mass from ecntre to infinity is
A−GMmRBGMmRC−GMm2RDGMmRA particle placed
1.inside a uniform spherical shell of mass M, but not at the center
2.inside a uniform spherical shell of mass M, at the center
3.outside a uniform spherical shell of mass M, a distance r from the center
4.outside a uniform solid sphere of mass M, a distance 2r from the center
If F1,F2,F3 and F4 are gravitational forces acting on the particle in four cases.AF1>F2>F3>F4BF1=F2<F3<F4CF1=F2<F4<F3DF1<F2<F3<F4
The work done to take a particle of mass m from surface of the earth to a height equal to 2R is
View SolutionA thin spherical shell of total mass M and radius R is held fixed. There is a small hole in the shell. A mass m is released from rest a distance R from the hole along a line that passes through the hole and also through the centre of the shell. This mass subsequently moves under the gravitational force of the shell. How long does the mass take to travel from the hole to the point diametrically opposite.
View SolutionStatement-1: Gravitational potential is zero inside a shell.
Statement-2: Gravitational potential is equal to the work done in bringing a unit mass from infinity to a point inside gravitational field.
View SolutionEach of the four corners of a square with edge a is occupied by a point mass m. There is a fifth mass, also m, at the center of the square. To remove the mass from the center to a point far away the work that must be done by an external agent is given by:
View Solution
Sphere of mass M and radius R is surrounded by a spherical shell of mass 2M and radius 2R as shown. A small particle of mass m is released from rest from a height h(<<R) above the shell. There is hole in the shell.
What time will it take to move from A to B?
View Solution

