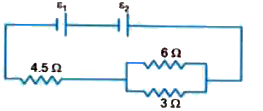
In the circuit diagram given in Fig. 4.31, the cells E1 and E2 have emf's 4 V and 8 V and internal resistances 0.5Ω and 10Ω respectively. Calculate the current in each resistance .
To solve the problem, we need to analyze the circuit and apply Kirchhoff's laws. Here's a step-by-step solution:
Step 1: Identify the Components
We have two cells:
- Cell E1: EMF = 4 V, Internal Resistance (r1) = 0.5 Ω
- Cell E2: EMF = 8 V, Internal Resistance (r2) = 10 Ω
We also need to identify the external resistances connected in the circuit. Let's assume there are resistances R1 and R2 connected in series with the cells.
Step 2: Write Kirchhoff's Loop Equation
Assuming the current flowing through the circuit is I, we can write the Kirchhoff's loop equation for the circuit. The total voltage provided by the cells must equal the total voltage drop across the resistances and internal resistances.
The loop equation can be written as:
E1−I⋅r1−I⋅R1−E2+I⋅r2+I⋅R2=0
Step 3: Substitute Known Values
Substituting the known values into the equation:
4−I⋅0.5−I⋅R1−8+I⋅10+I⋅R2=0
Step 4: Rearrange the Equation
Rearranging the equation gives:
I⋅(R1+R2+10−0.5)=4−8
I⋅(R1+R2+9.5)=−4
Step 5: Solve for Current I
To find the current I, we need the values of R1 and R2. Assuming R1 = R2 = R (for simplicity), we can substitute:
I⋅(2R+9.5)=−4
Step 6: Calculate Current
If we assume R = 0 (for simplification), we can calculate I:
I⋅9.5=−4
I=−49.5
This negative sign indicates the direction of current is opposite to our assumption.
Step 7: Find Current in Each Resistance
If we have the values of R1 and R2, we can substitute back to find the actual currents through each resistance.
Final Step: Conclusion
The current I can be calculated based on the actual values of R1 and R2. If R1 and R2 are known, substitute them back into the equation to find the current through each resistance.
We have two cells:
- Cell E1: EMF = 4 V, Internal Resistance (r1) = 0.5 Ω
- Cell E2: EMF = 8 V, Internal Resistance (r2) = 10 Ω
Assuming the current flowing through the circuit is I, we can write the Kirchhoff's loop equation for the circuit. The total voltage provided by the cells must equal the total voltage drop across the resistances and internal resistances.
E1−I⋅r1−I⋅R1−E2+I⋅r2+I⋅R2=0
Substituting the known values into the equation:
4−I⋅0.5−I⋅R1−8+I⋅10+I⋅R2=0
Rearranging the equation gives:
I⋅(R1+R2+10−0.5)=4−8
I⋅(R1+R2+9.5)=−4
To find the current I, we need the values of R1 and R2. Assuming R1 = R2 = R (for simplicity), we can substitute:
I⋅(2R+9.5)=−4
If we assume R = 0 (for simplification), we can calculate I:
I⋅9.5=−4
I=−49.5
This negative sign indicates the direction of current is opposite to our assumption.
If we have the values of R1 and R2, we can substitute back to find the actual currents through each resistance.
The current I can be calculated based on the actual values of R1 and R2. If R1 and R2 are known, substitute them back into the equation to find the current through each resistance.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - SL ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - Problems From Competitive
18 Videos
- CURRENT ELECTRICITYBOOK - SL ARORACHAPTER - CURRENT ELECTRICITYEXERCISE - Problems For Self
101 Videos
- CHEMICAL EFFECT OF CURRENTBOOK - SL ARORACHAPTER - CHEMICAL EFFECT OF CURRENTEXERCISE - TYPE-B
5 Videos
- ELECTRIC POTENTIAL AND ELECTRIC FLUXBOOK - SL ARORACHAPTER - ELECTRIC POTENTIAL AND ELECTRIC FLUXEXERCISE - Problems for self practive
61 Videos
Similar Questions
In the circuit shown in Fig. 4.68, the cells ε1 and ε2 have emf's of 4 V and 8 V and internal resistances of 0.5Ω and 1Ω respectively. Calculate the current in each resistance.
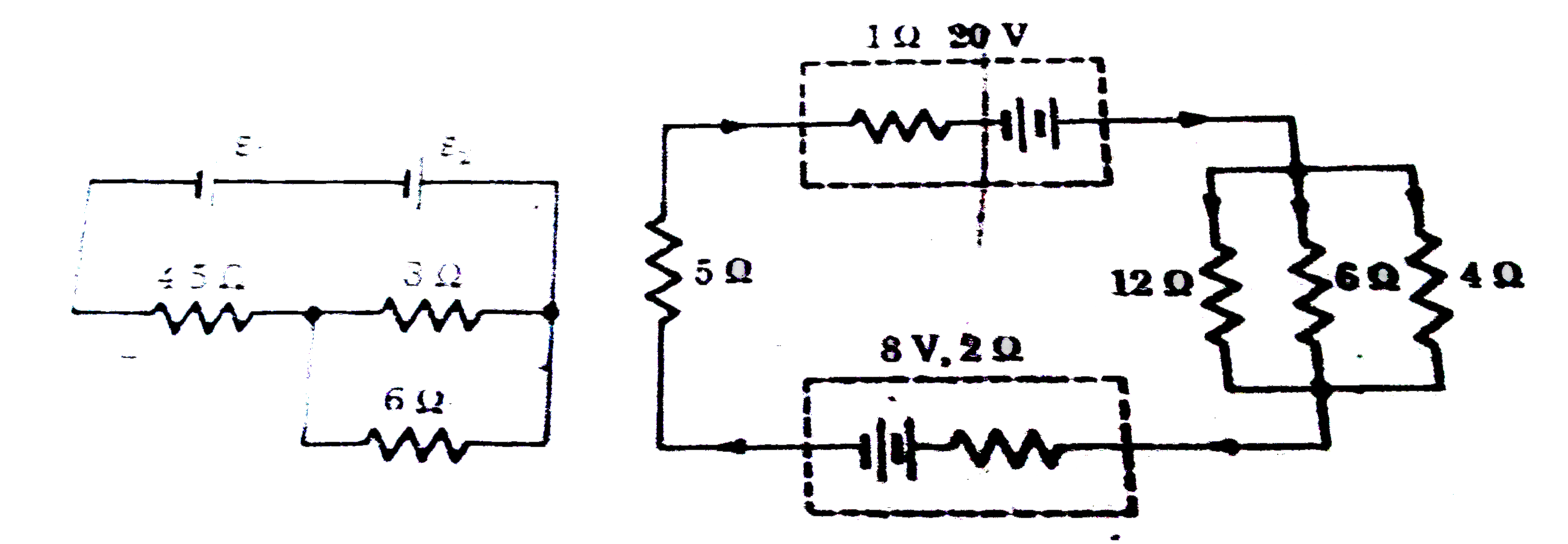
View SolutionIn the circuit, the cells E1andE2 have emfs of 4V and 8V and internal resistance 0.5Ωand1.0Ω, respectively. Calculate the current through 6Ω resistance.
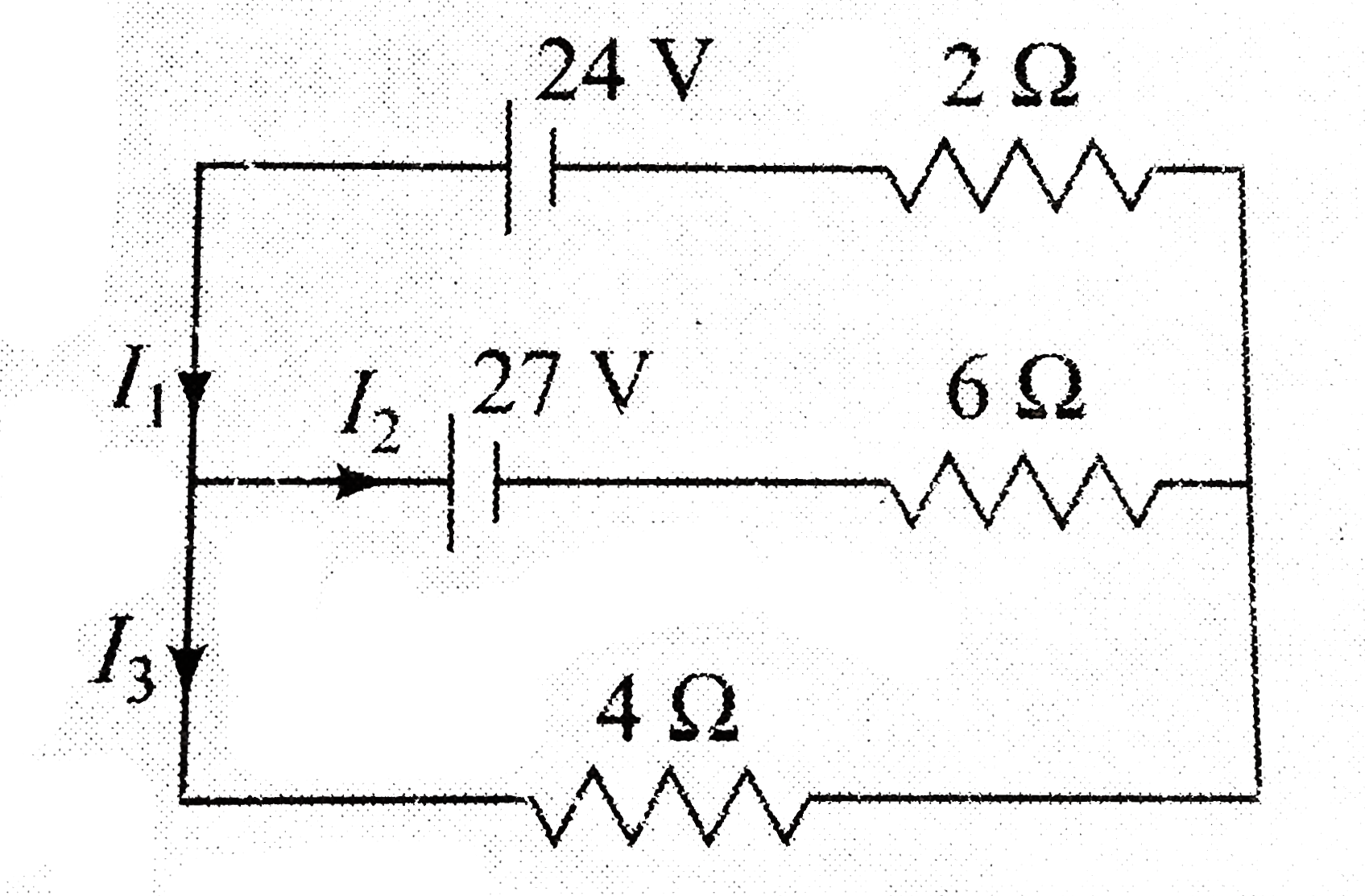
View Solution
Knowledge Check
In the circuit shown E,F,G and H are cells of emf 2V,1V,3V and 1V respectively and their internal resistance are 2Ω,1Ω,3Ω and 1Ω respectively.
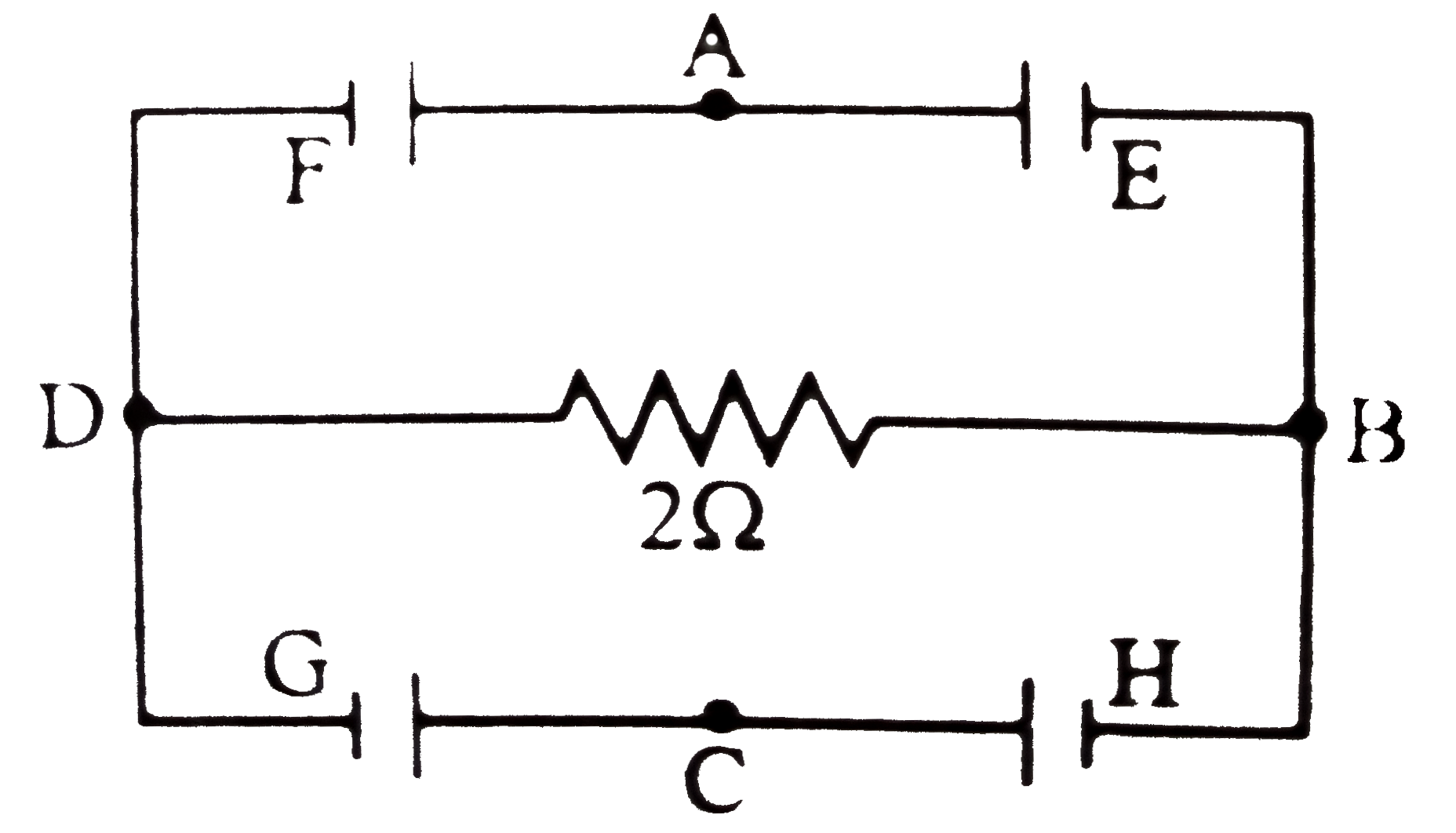 AVD−VB=−2/13VBVD−VB=2/13VCVG=21/13V=potential difference across GDVH=19/13V=potential difference across H
AVD−VB=−2/13VBVD−VB=2/13VCVG=21/13V=potential difference across GDVH=19/13V=potential difference across H
Two cells of emfs 1.5 V and 2.0 V having internal resistances 0.2Ω and 0.3Ω respectively are connected in parallel. Calculate the emf and internal resistance of the equivalent cell.
View SolutionTwo cells E1 and E2 in the circuit shown in figure, have emfs of 5 V and 9 V and internal resistance of 0.3Ω and 1.2Ω respestivley. Calculate the value of current flowing through the resistance of 3Ω.
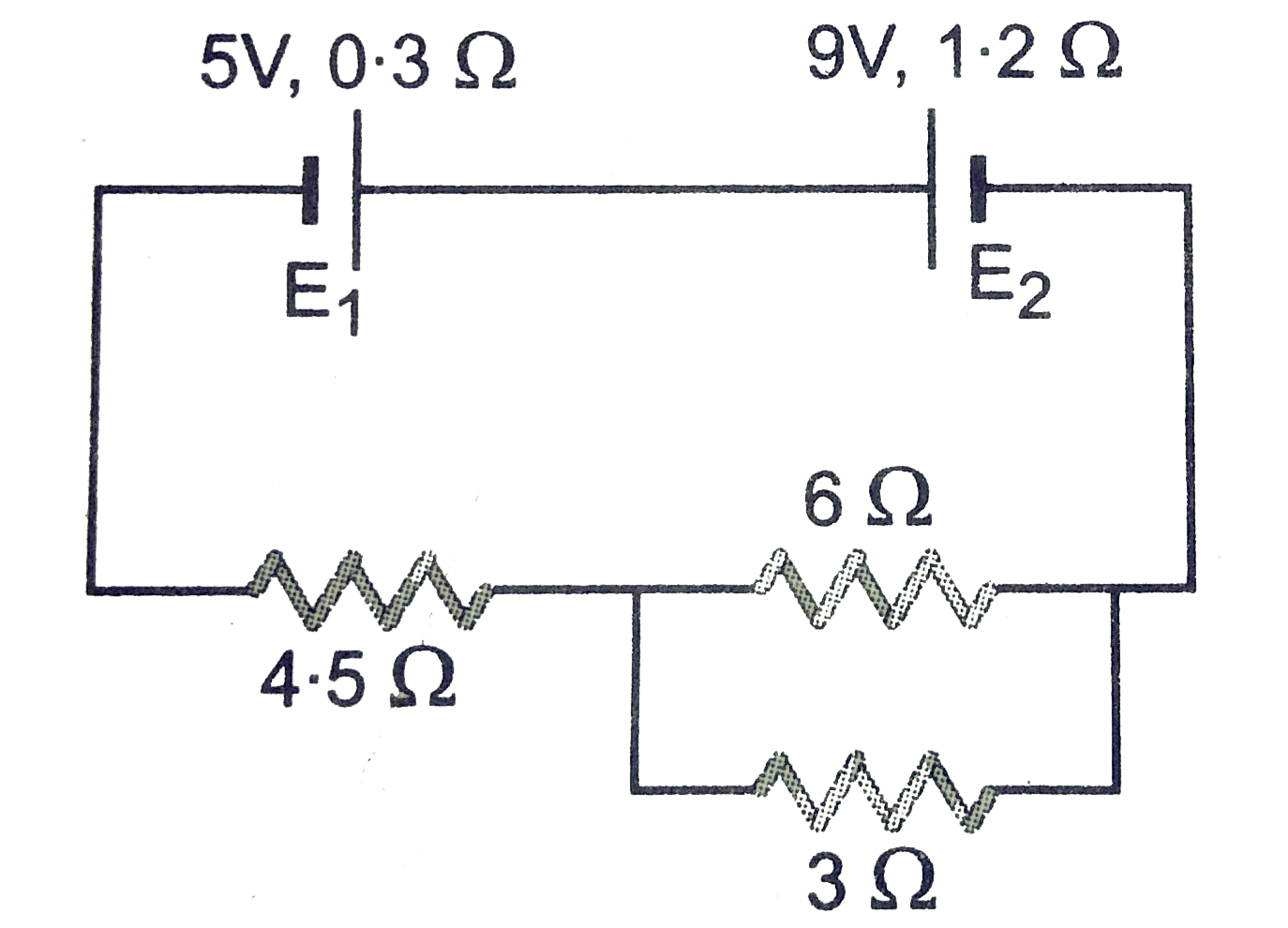
View SolutionTwo cells ε1 and ε2 in the given circuit diagram have an emf of 5 V and 9 V and internal resistance of 0.3 Ω and 1.2Ω respectively. Calculate the value of current flowing through the resistance of 3 Ω .
View SolutionTwo cells of emfs 1.5 V and 2.0v having internal resistance 0.2Σ and 0.3 Σ respectively are connected in parallel . Calculate the emf and internal resistance of the equivalent cell .
View SolutionTwo cells E1 and E2 of emfs 4 V and 8 V having internal resistances 0.5Ω and 1.0Ω respectively are connected in opposition to each other. This combination is connected in series with resistances of 4.5Ω and 3.0Ω. Another resistance is connected in parallel across the 3Ω resistor.
(a) Draw the circuit diagram
(b) Calculate the total current flowing through the circuit.
View SolutionA battery is formed by connecting three cells in series .
The emfs of cells are 5 V, 2.5 V and 1.5 V and their internal resistance are 0.5Ω,0.05Ωand0.45Ω respectively.
This battery is connected across a load resistance of 5Ω what current will be supplied by the battery ? if the cell of emf 1.5 V were connected with reverse polarity then what would have been the current supplied by the battery ?
View SolutionThree cells are connected in parallel, with their like poles connected together, with wires of negligible resistance. If the emf of the cell are 2V, 1V and 4V and if their internal resistance are 4Ω,3Ωand2Ω respectively, find the current through each cell.
View Solution
