Determine the voltage drop across the resistor R1 in the circuit given below with E=60V,R1=18Ω,R2=10Ω.
To determine the voltage drop across the resistor R1 in the given circuit, we will follow these steps:
Step 1: Identify the resistances and the voltage source
We have:
- E=60V (the voltage source)
- R1=18Ω
- R2=10Ω
Step 2: Calculate the equivalent resistance of R1 and R2
Since R1 and R2 are in parallel, we can use the formula for the equivalent resistance Req of two resistors in parallel:
1Req=1R1+1R2
Substituting the values:
1Req=118+110
Finding a common denominator (which is 90):
1Req=590+990=1490
Thus,
Req=9014=457≈6.43Ω
Step 3: Calculate the total resistance in the circuit
The equivalent resistance Req is in series with R1:
Rtotal=Req+R1=457+18
To add these, convert 18 to a fraction with a denominator of 7:
Rtotal=457+1267=1717≈24.43Ω
Step 4: Calculate the total current in the circuit
Using Ohm's Law, V=IR, we can find the total current I:
I=ERtotal=601717=60×7171≈2.51A
Step 5: Calculate the voltage drop across R1
Now, we can find the voltage drop VR1 across R1 using Ohm's Law again:
VR1=I×R1=2.51×18≈45.18V
Thus, the voltage drop across the resistor R1 is approximately 45V.
Summary
The voltage drop across the resistor R1 is approximately 45V.
---
We have:
- E=60V (the voltage source)
- R1=18Ω
- R2=10Ω
Since R1 and R2 are in parallel, we can use the formula for the equivalent resistance Req of two resistors in parallel:
The equivalent resistance Req is in series with R1:
Using Ohm's Law, V=IR, we can find the total current I:
Now, we can find the voltage drop VR1 across R1 using Ohm's Law again:
The voltage drop across the resistor R1 is approximately 45V.
Topper's Solved these Questions
- CURRENT ELECTRICITYBook:SL ARORAChapter:CURRENT ELECTRICITYExercise:Problems From Competitive
Explore 18 Videos
- CURRENT ELECTRICITYBook:SL ARORAChapter:CURRENT ELECTRICITYExercise:Problems For Self
Explore 101 Videos
- CHEMICAL EFFECT OF CURRENTBook:SL ARORAChapter:CHEMICAL EFFECT OF CURRENTExercise:TYPE-B
Explore 5 Videos
- ELECTRIC POTENTIAL AND ELECTRIC FLUXBook:SL ARORAChapter:ELECTRIC POTENTIAL AND ELECTRIC FLUXExercise:Problems for self practive
Explore 61 Videos
Similar Questions
Determine the voltage drop across the resistor R1 in the circuit given below with E = 65V, R_1 = 50 OmegaR_2 = 100 Omega, R_3 = 100 Omega, and R_4 300 Omega.

View SolutionDetermine the voltage drop across the resistance R1 in the circuit given in Fig. 4.55 with ε=90V,R1=5kΩ,R2=5kΩ,R3=10kΩ and R4=10kΩ.
View Solution
Knowledge Check
The potential difference in volt across the resistance R3 in the circuit shown in figure, is (R1=15Ω,R2=15Ω,R3=30Ω,R4=35Ω)
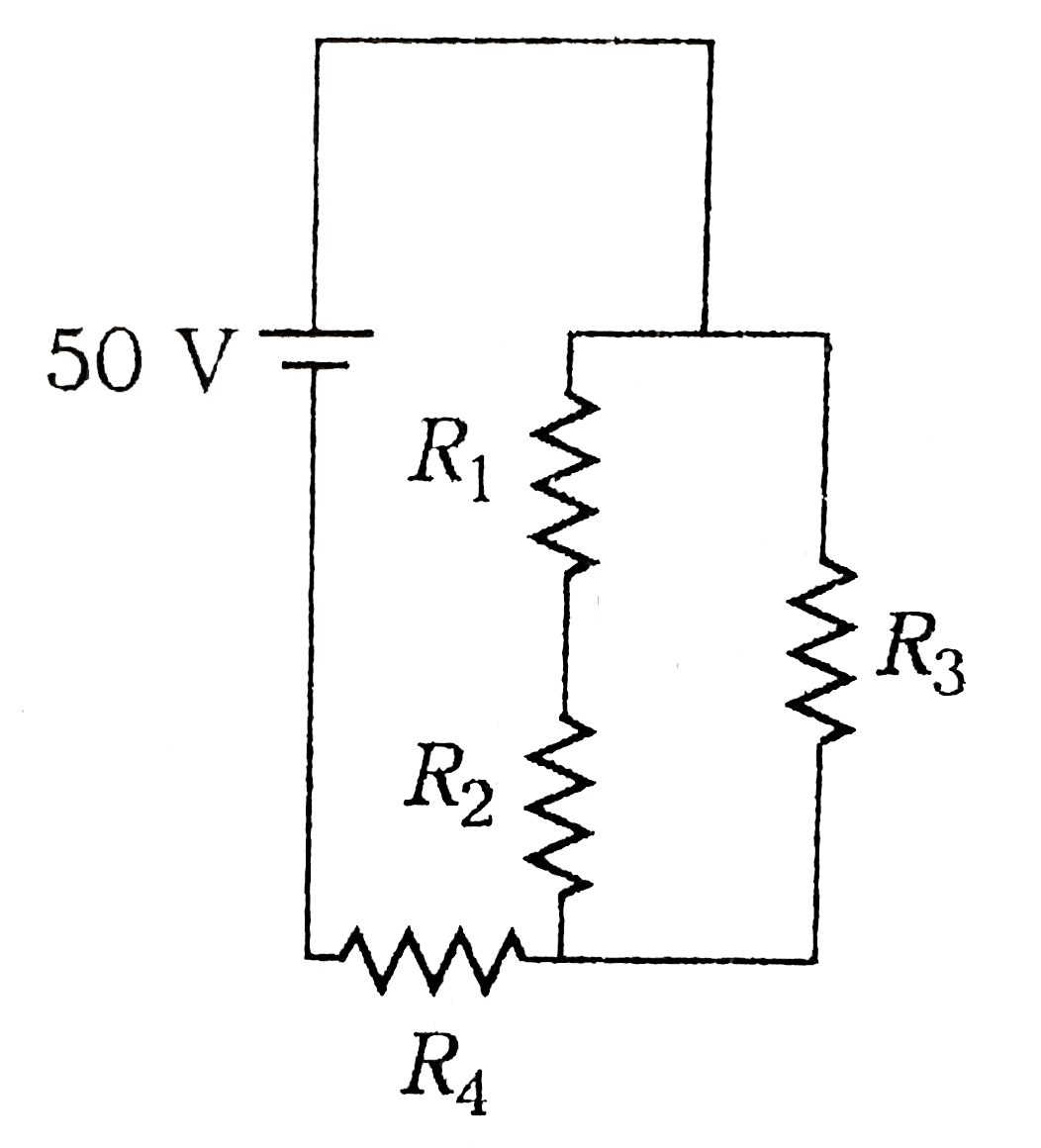 A5B7.5C15D12.5
A5B7.5C15D12.5An alternating voltage V=100sinωt is applied across an LCR circuit as shown. At the instant when voltage drop across source is 50√3 volts then at that instant
R=30Ω XL=60Ω XC=20Ω
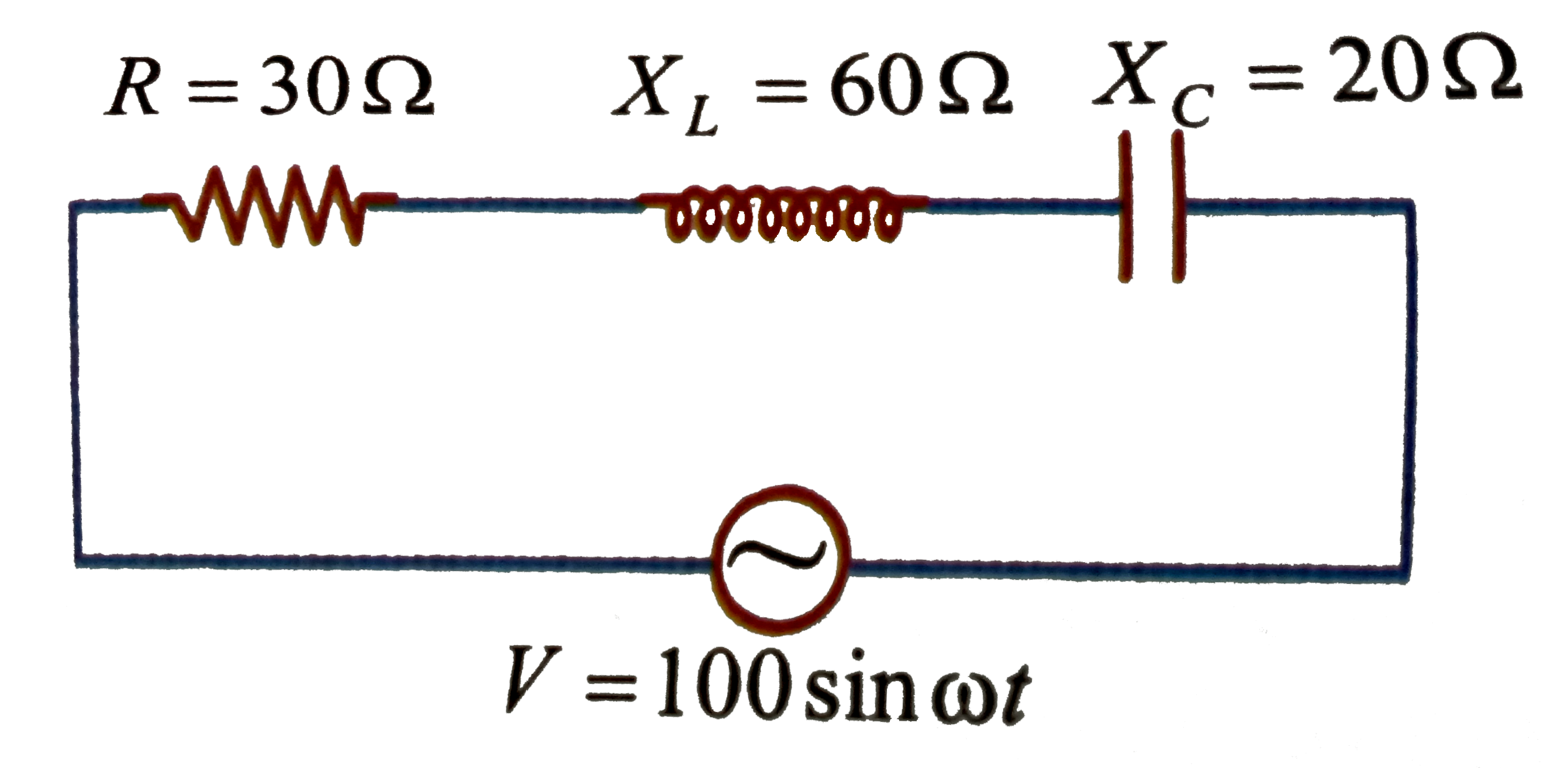 Avoltage drop across inductor is (120cos7∘) voltsBvoltage drop across capacitor is (40cos173∘) voltsCvoltage drop across resistor is (60cos7∘) voltsDAll the above
Avoltage drop across inductor is (120cos7∘) voltsBvoltage drop across capacitor is (40cos173∘) voltsCvoltage drop across resistor is (60cos7∘) voltsDAll the aboveFind the time constant (in μs) for the given RC circuits in the given order respectively.
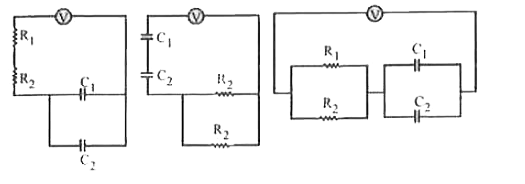
R1=1ω,R2=2ω,C1=4μF,C2=2μFA18,4,89B18,89,4C4,18,89D4,89,18
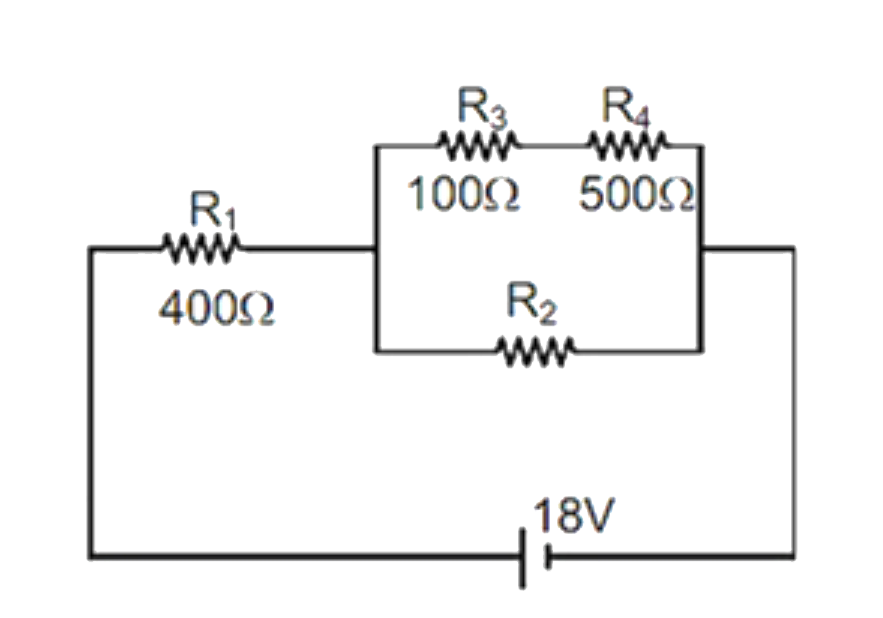
If the voltage across 500Ω is 5 V. then R2 is
View SolutionFind a potentail difference φ1−φ2 between points 1 and 2 of the circuit shown in Fig if R11=10Ω,R2=20Ω,E1=5.0V, and E2=2.0V. The internal resisances of the current sources are negligible.

View Solution(a) Resistors given as R1,R2andR3 are connected in series to a battery V. Draw the circuit diagram showing the arrangement. Derive an expression for the equivalent resistance of the combination.
(b) If R1=10Ω,R2=20ΩandR3=30Ω, calculate the effective resistance when they are connected in series to a battery of 6 V. Also find the current flowing in the circuit.
View Solution
In the given cirucit, determine current through branch having indicated resistor R4 Given R1=R2=4Ω,R3=R4
R5=2Ωε1=5V,ε2=10V
View SolutionIn the circuit shown, the voltage drop across the 15Ω resistor is 30V having the polarity as indicated. The ratio of potential difference across 5Ω resistor and resistance R is :
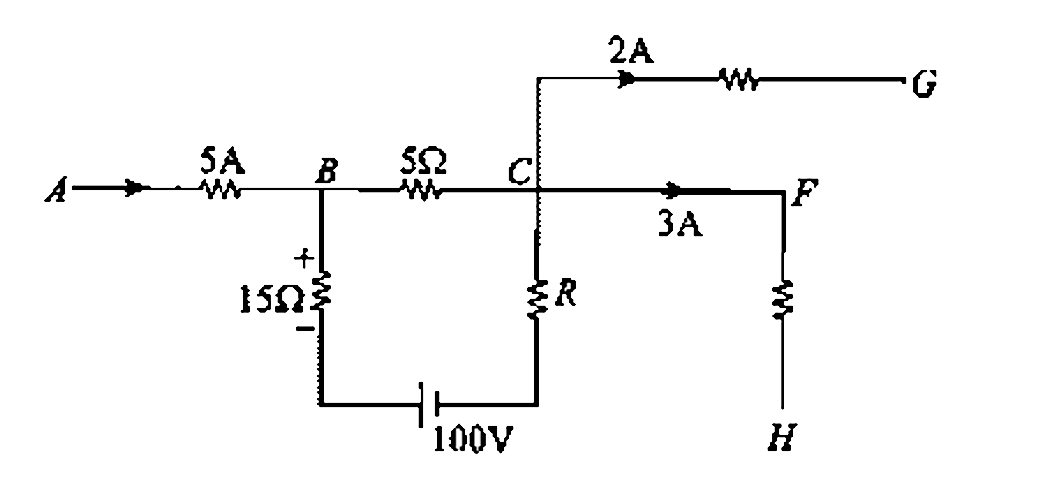
View Solution

