The energy stored in a capacitor of capacitance 100μF is 50 J. Its potential difference is
50 V
500 v
1000 V
1500 V
The correct Answer is:C
To find the potential difference across a capacitor given its capacitance and the energy stored, we can use the formula for the energy stored in a capacitor:
U=12CV2
Where:
- U is the energy stored in the capacitor (in joules),
- C is the capacitance (in farads),
- V is the potential difference (in volts).
Step 1: Write down the known values
Given:
- U=50J
- C=100μF=100×10−6F
Step 2: Substitute the known values into the energy formula
Substituting the values into the formula:
50=12×(100×10−6)×V2
Step 3: Simplify the equation
Multiply both sides by 2 to eliminate the fraction:
100=(100×10−6)×V2
Step 4: Divide both sides by 100×10−6
To isolate V2:
V2=100100×10−6=1000.0001=106
Step 5: Take the square root of both sides
Now, taking the square root to find V:
V=√106=1000V
Conclusion
The potential difference across the capacitor is:
V=1000V
- U is the energy stored in the capacitor (in joules),
- C is the capacitance (in farads),
- V is the potential difference (in volts).
Given:
- U=50J
- C=100μF=100×10−6F
Substituting the values into the formula:
Multiply both sides by 2 to eliminate the fraction:
To isolate V2:
Now, taking the square root to find V:
The potential difference across the capacitor is:
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEYChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:(A) Chapter exercises
Explore 229 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEYChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:(B) Chapter exercises
Explore 20 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBook:DC PANDEYChapter:ELECTROSTATIC POTENTIAL AND CAPACITORSExercise:Check point 2.4
Explore 15 Videos
- ELECTROMAGNETIC WAVESBook:DC PANDEYChapter:ELECTROMAGNETIC WAVESExercise:Sec C
Explore 22 Videos
- ELECTROSTATICSBook:DC PANDEYChapter:ELECTROSTATICSExercise:Medical entrances gallery
Explore 37 Videos
Similar Questions
Write the expression for energy stored in a capacitor in terms of capacitance and potential difference between the plates.
View SolutionA capacitor of capacitance 5 μF is charged to a potential difference of 10 volts and another capacitor of capacitance 9 μF is charged to a potential difference of 8 volts. Now these two capacitors are connected in such a manner that the positive plate of one is connected to the positive plate of other. Calculate the common potential difference across the two capacitors.
View Solution
Knowledge Check
Find the energy stored in a capacitor of capacitance 100μF when it is charged to a potential difference of 20 V.
A0.02JB0.04JC0.01JD0.05JIf the energy of a capacitor of capacitance 2μF is 0.16 joule. Then its potential difference will be
A800VB400VC16×104VD16×10−4VA capacitor of capacitance 50μF is charged to 10 V. Its electrostatic potential energy is
A2.5×10−3JB2.5×10−4JC5×10−2JD1.2×10−5J
Consider the following network of capacitors. The capacitances are marked in the figure. If emnergy stored in the capacitor of capacitance 6μF is E, then what will be the total amount of energy stored in the system?

View SolutionA parallel plate capacitor of capacitance 2 μF is fully charged to a potential difference of 500 volts and then disconnected from the battery. Using insulating handles, separation between the paltes is made thrice the initial value. What will be the new potential difference between the plates of the capacitor and by what amount stored energy changes in this process?
View SolutionThe charge and energy stored in the capacitor of capacity 32μF, when it is charged to a potential difference of 0.6 kV are respectively
View SolutionTwo capacitors of capacitances 3μFand5μF respectively are connected in parallel and this combination is connected in series with a third capacitor of capacitance 2μF. A potential difference of 100 V is applied across the entire combination. The charge and the potential difference across the third capacitor is
View SolutionCalculate the energy stored in the capacitor of capacitance 2μf. The voltmeter gives a reading of 15 V and the ammeter A reads 15mA .
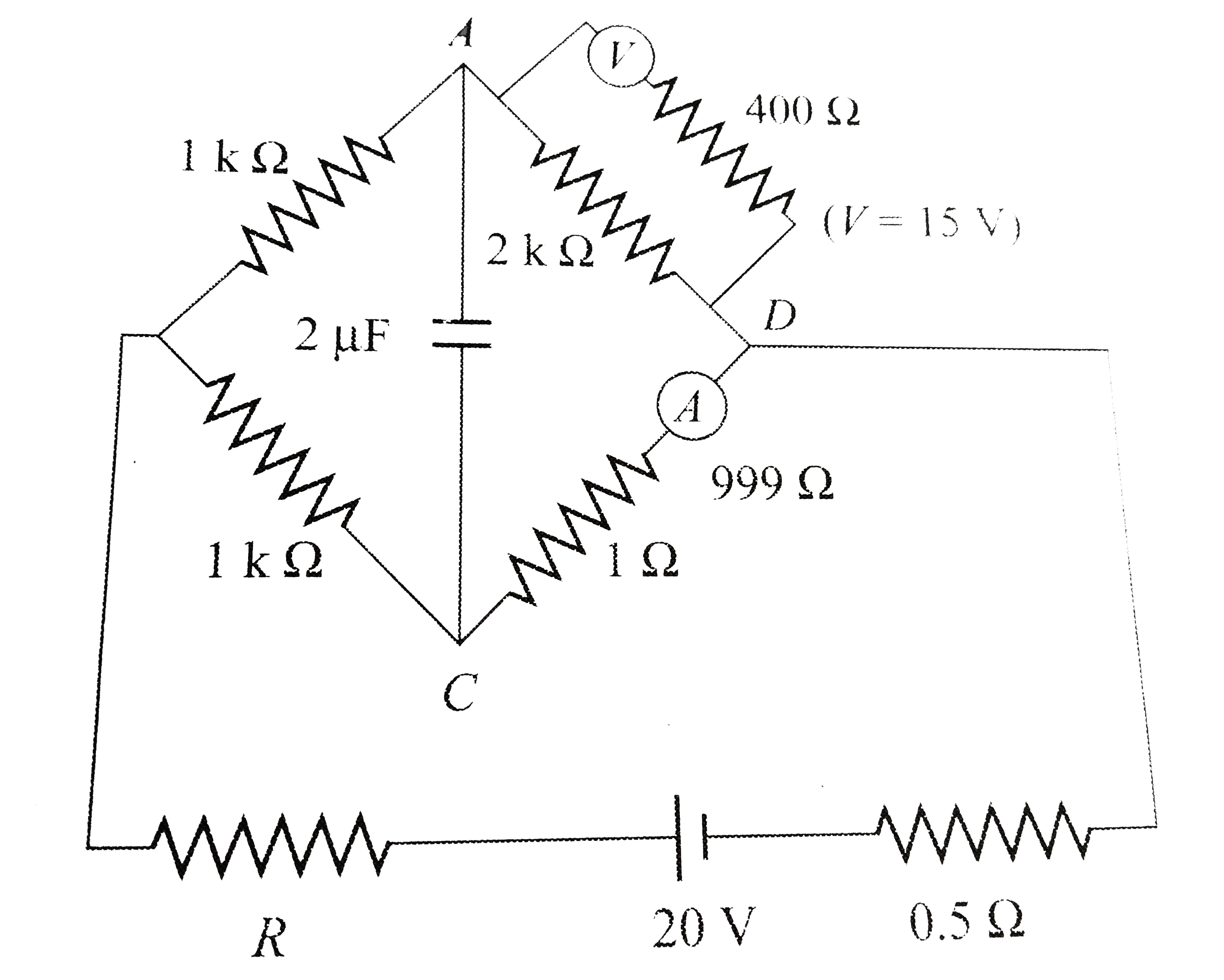
View Solution

