From what distance should a 100 eV electron be fired towards a large metal plate having a surface charge of −2.0×10−6Cm−2, so that it just fails to strike the plate ?
0.50 mm
0.44 m
0.60 mm
0.77 mm
The correct Answer is:B
To solve the problem step by step, we will use the concepts of electric field, potential difference, and energy conservation.
Step 1: Understand the Given Data
We have:
- Energy of the electron, E=100eV
- Surface charge density of the plate, σ=−2.0×10−6C/m2
Step 2: Convert Energy from eV to Joules
1 eV is equal to 1.6×10−19J. Therefore, we convert the energy of the electron:
E=100eV=100×1.6×10−19J=1.6×10−17J
Step 3: Calculate the Electric Field (E) due to the Charged Plate
The electric field E due to a large charged plate is given by the formula:
E=σϵ0
where ϵ0 (the permittivity of free space) is approximately 8.85×10−12C2/N m2.
Substituting the values:
E=−2.0×10−68.85×10−12≈−226.5N/C
Step 4: Relate Electric Field to Potential Difference
The potential difference V between two points in an electric field is given by:
V=E⋅d
where d is the distance from the plate.
Step 5: Relate Energy to Work Done
The work done on the electron when it moves through a potential difference V is equal to its energy:
W=qV
where q is the charge of the electron, approximately −1.6×10−19C.
Setting the work done equal to the energy of the electron:
1.6×10−17=(−1.6×10−19)⋅V
Step 6: Substitute for V
From the previous equation, we can express V as:
V=1.6×10−17−1.6×10−19=−100V
Step 7: Substitute V into the Electric Field Equation
Now, substituting V back into the electric field equation:
−100=(−226.5)⋅d
Solving for d:
d=−100−226.5≈0.441m
Step 8: Convert Distance to Millimeters
To convert meters to millimeters:
d≈0.441m×1000mm/m=441mm
Step 9: Final Answer
The distance from which the electron should be fired is approximately 0.44mm.
Conclusion
Thus, the answer is 0.44mm, which corresponds to option 2.
We have:
- Energy of the electron, E=100eV
- Surface charge density of the plate, σ=−2.0×10−6C/m2
1 eV is equal to 1.6×10−19J. Therefore, we convert the energy of the electron:
E=100eV=100×1.6×10−19J=1.6×10−17J
The electric field E due to a large charged plate is given by the formula:
E=σϵ0
where ϵ0 (the permittivity of free space) is approximately 8.85×10−12C2/N m2.
E=−2.0×10−68.85×10−12≈−226.5N/C
The potential difference V between two points in an electric field is given by:
V=E⋅d
where d is the distance from the plate.
The work done on the electron when it moves through a potential difference V is equal to its energy:
W=qV
where q is the charge of the electron, approximately −1.6×10−19C.
1.6×10−17=(−1.6×10−19)⋅V
From the previous equation, we can express V as:
V=1.6×10−17−1.6×10−19=−100V
Now, substituting V back into the electric field equation:
−100=(−226.5)⋅d
Solving for d:
d=−100−226.5≈0.441m
To convert meters to millimeters:
d≈0.441m×1000mm/m=441mm
The distance from which the electron should be fired is approximately 0.44mm.
Thus, the answer is 0.44mm, which corresponds to option 2.
Topper's Solved these Questions
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Taking it together
105 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Assertion and Reason
15 Videos
- ELECTROSTATICSBOOK - DC PANDEYCHAPTER - ELECTROSTATICSEXERCISE - Check point 1.4
10 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITORSBOOK - DC PANDEYCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITORSEXERCISE - (C) Chapter exercises
50 Videos
- GRAVITATIONBOOK - DC PANDEYCHAPTER - GRAVITATIONEXERCISE - All Questions
120 Videos
Similar Questions
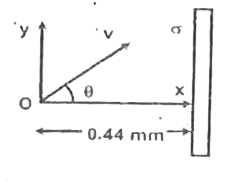
An electron is projected with a velocity of 1.186×107m/s at an angle θ with the x-axis, towards a large metallic plate kept 0.44 mm away from the electron. The plate has a surface charge density −2×10−6C/m2. Find the minimum value of θ, for which it fails to strike the plate.
View SolutionA small piece of cesium metal is kept at a distance of 20 cm form a large metal plate having a charge density of 1.0×(10−9)C(m−2) on the surface facing the cesium piece. A monochromatic light of wavelength 400nm is incident on the cesium piece. Find the minimum and the maximum kinetic energy of the photoelectrons reaching the large metal plate. Neglect any change in electric field due to the small piece of cesium present.
View Solution
Knowledge Check
A circular metal plate of radius 10 cm is given a charge of 20μC on its surface. The charge density of the plate is
A3.185×10−6C/m2B2×10−6C/m2C3×10−9C/m2D3.184×10−4C/m2A metal plate of area 2m2 is charged with 12×10−6C. The surface surface density of charge is
A3μC/m2B4μC/m2C6μC/m2D8μC/m2An electron is projected as in figure with kinetic energy K, at an angle θ=45∘ between two charged plates. The magnitude of the electric field so that the electron just fails to strike the upper plate, should be greater than:
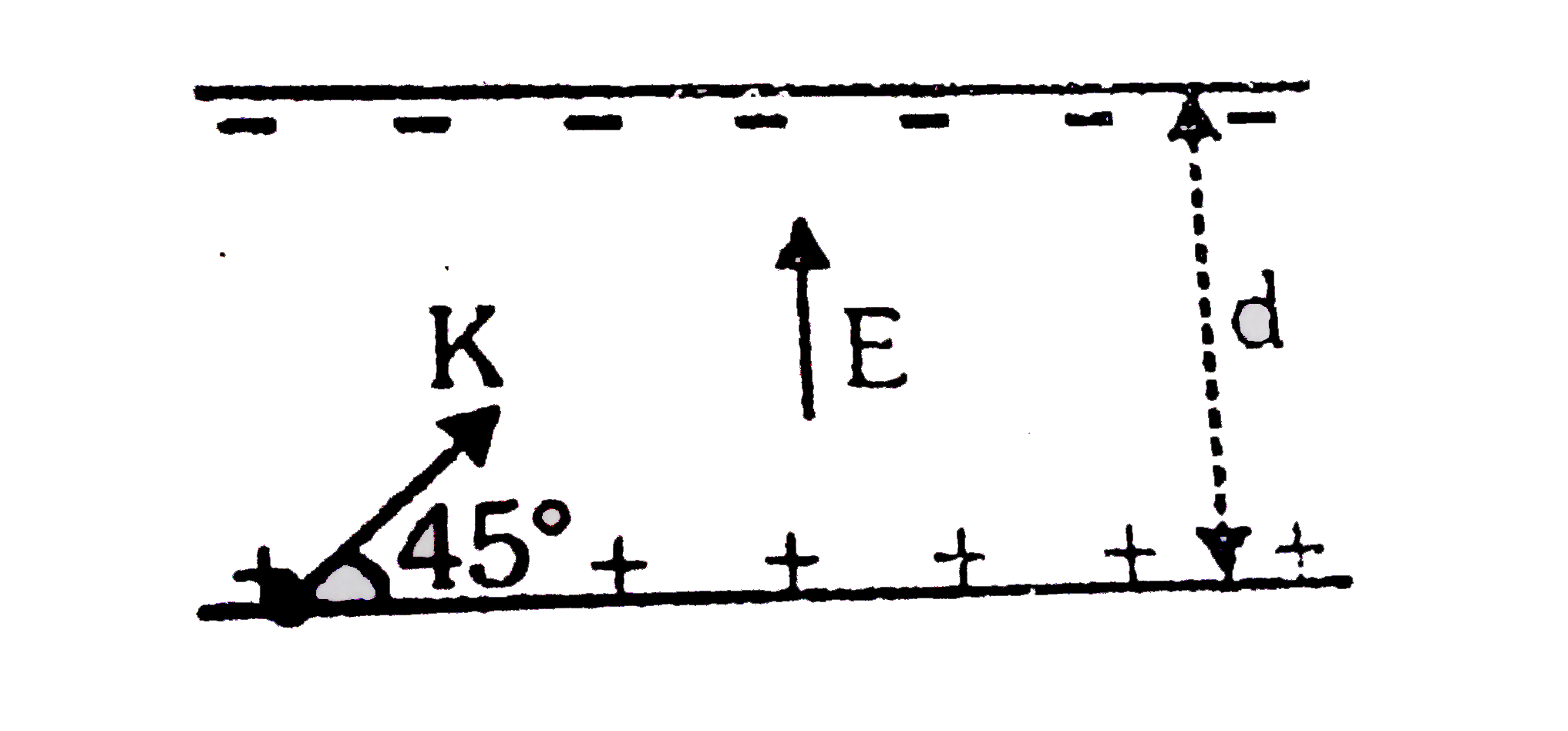 AKqdB2KqdCK2qdDiInifinite
AKqdB2KqdCK2qdDiInifinite
An electric is fired directly towards the center of a large metal plate that has excess negative charge with surface charge density =2.0×10−6C/m2. If the initial kinetic energy of electron of electron is 100 eV and if it is to stop due to repulsion just as it reaches the plate, how far from the plate must it be fired ?
View SolutionA charged partical having a charge of −2.0×10−6C is placed close to a nonconducting plate having a surface charge density 4.0 xx 10^(6) C m^(-2). Fine the force of attraction between the particle and the plate.
View SolutionTwo large, thin metal plates are parallel and close to each other. On their inner faces, the plates have surface charge densities of opposite signs and of magnitude 19×10−22Cm−2.
What is E (a) to the left of the plates (b) to the right of the plates (c) between the plates ?
Here, σ=19×10−22Cm−2
View SolutionA parallel plate capacitor has circular plates each of radius 5.0 cm. It is being charged so that electric field in the gap between its plates rises steadily at the rate of 2×1012Vm−1s−1What is the displacement current.
View SolutionWhen 1020 electrons are removed from the surface of a neutral metal plate, the electric charge on it (in coulomb) is
View Solution
