Assertion One end of a massless rod of length l is hinged so that it is free to rotate in vertical plane about a horizontal axis. If a particle is attached to the other end of the rod, then the minimum speed at lower most position of the particle is √5gl to complete the circular motion.
Reason Work done by cnetripetal force on the particle is always zero.
If both Assertion and Reason are correct and Reason is the correct explanation of Assertion.
If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
If Assertion is true but Reason is false.
If Assertion is false but Reason is true.
The correct Answer is:D
In case of massless rod, vmin=√4gl.
Work done by centripetal force on the particle is always zero.
Similar Questions
A rod of length l is released from the vertical position on a smooth horizontal plane. What is the nature of motion of the free end of the rod ?
View SolutionOne end of a light rod is clamped in such a manner that rod can be rotated in a vertical plane . A block of mass mis attached to the other ened of rod and the block stays at rest at its lowest position . What minimum speed should be imparted to the bock so that it may complete its circle ? Assume length of rod to be l .
View Solution
Knowledge Check
A light rigid rod of length l is hinged at one end and it is free to rotate in a vertical plane. A particle of mass m is sattached to anothr and of the rod. The particle is released from rest at its highest point. Select the correct statement out of the following
ATension in the rod is zero when it makes an angle of cos−1(13) with the verticalBTension in the rod is zero when it makes an angle of cos−1(23) with the verticalCSpeed of partical of mass m is √23gl when the tension in the rod is zeroDSpeed of particle of mass m is √43gl when the tension in the rod is zeroA particle is rotated in a vertical circle by connecting it to a string of length l and keeping the other end of the string fixed. The minimum speed of the particle when the string is horizontal for which the particle will complete the circle is
A√glB√2glC√3glD√5glOne end of a uniform rod of length l and mass m is hinged at A. It is released from rest from horizontal position AB as shown in figure. The force exerted by the rod on the hinge when it becomes vertical is
 A32mgB52mgC3mgD5mg
A32mgB52mgC3mgD5mg
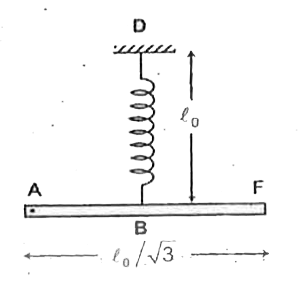
In the figure shown one end of a light spring of natural length l0=√58m(≈0.8m) is fixed at point D and other end is attached to the centre B of a uniform rod AF of length l0/√3 and mass 10kg. The rod is free to rotate in a vertical plane about a fixed horizontal axis passing through the end A of the rod. The rod is held at rest in horizontal position and the spring is in relaxed state. It is found that, when the rod is released to move it makes an angle of 60∘ with the horizontal when it comes to rest for the first time. Find the
(a) the maximum elogation in the spring . (Approximately)
(b) the spring constant. (Approximately)
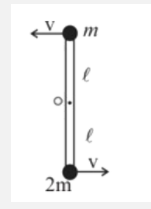
View SolutionTwo particles of masses m and 2m are attached to the massless rod of length 2l as shown in figure. The rod is hinged at its midpoint O and is free to rotate in vertical plane about hinge. The minimum speed v at the given instant so that it can complete the circle.
View SolutionA rod AB is 1 m long. It is hinged at A so as to rotate in a vertical plane. Initially the rod is horizontally placed and then it is released from rest Obtain the angular speed of the rod and the linear speed of its free end as it passes through the position shown in the diagram.
View SolutionA massless rod of length l is hinged at one end and is held horizontal by two identical vertical wires, which are tied at distances a and b form the hinged end. A load P si applied at the free end of the rod.
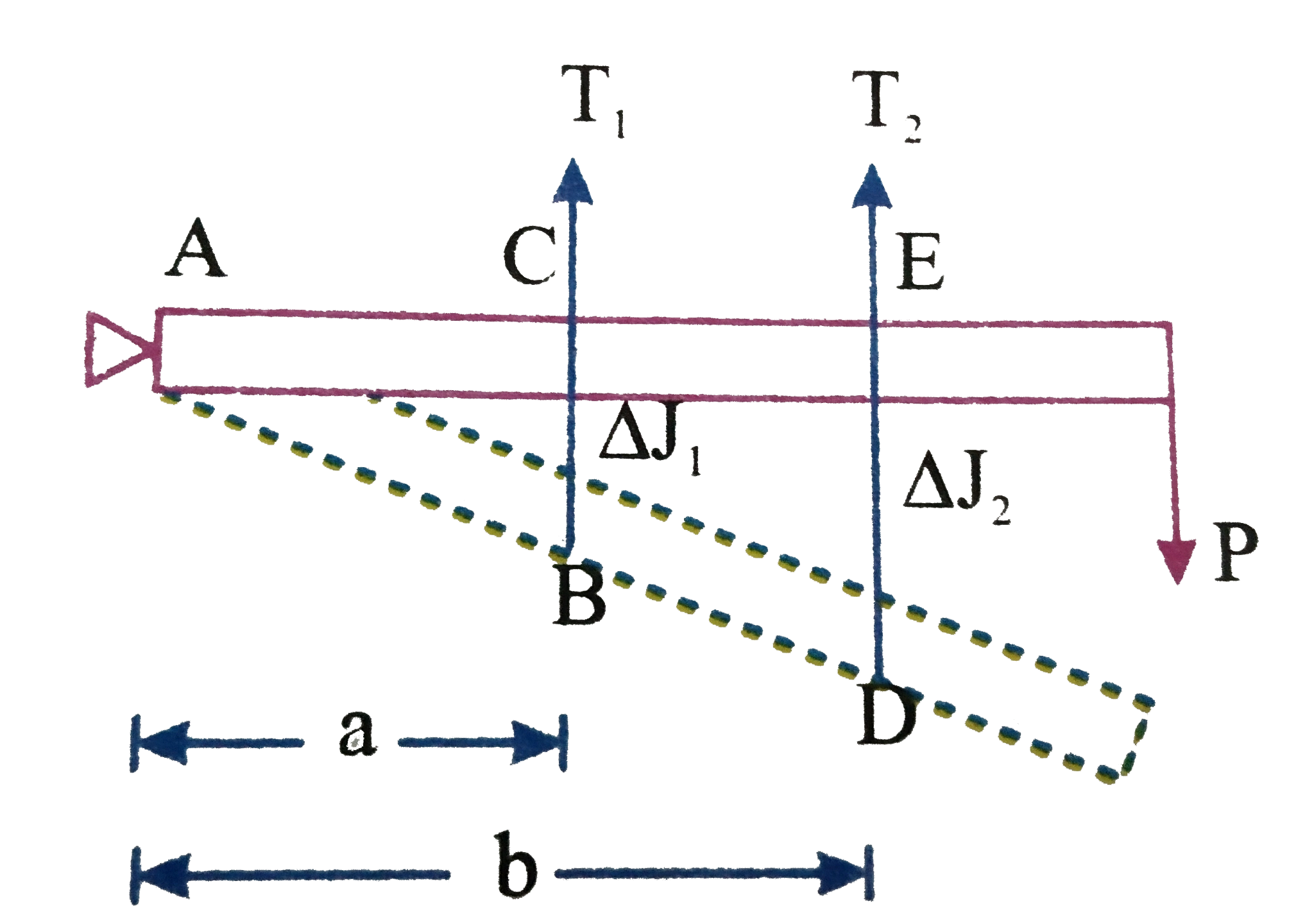
The tension in the first is
View SolutionA uniform rod of mass m and length l is hinged at upper end. Rod is free to rotate in vertical plane. A bail of mass m moving horizontally with velocity v0 collides at lower end of rod perpendicular to it and sticks to it. The minimum velocity of the ball such that combined system just completes the vertical circle will be
View Solution

