A small sphere of mass m is supended by a thread of length l. It is raised upto the height of suspension with thread fully stretched and released. Then, the maximum tension in thread will be
mg
2 mg
3 mg
6 mg
The correct Answer is:C
To solve the problem of determining the maximum tension in the thread when a small sphere of mass m is suspended and released from a height equal to the length of the thread l, we can follow these steps:
1. Understanding the Initial Conditions:
- The sphere is raised to the height l (the length of the thread) and then released. At this point, the potential energy is at its maximum, and the kinetic energy is zero.
2. Calculating Initial Potential Energy:
- The potential energy (PE) at the height l is given by:
PE=mgh=mgL
- Here, h=l is the height from which the sphere is released.
3. Conservation of Energy:
- As the sphere falls, the potential energy converts into kinetic energy (KE). At the lowest point, all the potential energy will have converted into kinetic energy.
- The kinetic energy at the lowest point is:
KE=12mv2
- By conservation of energy:
mgL=12mv2
4. Solving for Velocity:
- Rearranging the energy equation gives:
v2=2gL
- Thus, the velocity v at the lowest point is:
v=√2gL
5. Calculating the Forces at the Lowest Point:
- At the lowest point, the tension T in the thread must counteract both the weight of the sphere and provide the centripetal force required for circular motion.
- The weight of the sphere is mg.
- The centripetal force needed is given by:
Fc=mv2R
- Here, R=L (the radius of the circular path).
6. Substituting for Centripetal Force:
- Substituting v2:
Fc=m(2gL)L=2mg
7. Finding the Total Tension:
- The total tension in the thread at the lowest point is:
T=mg+Fc=mg+2mg=3mg
8. Conclusion:
- Therefore, the maximum tension in the thread when the sphere is at the lowest point is:
Tmax=3mg
Final Answer:
The maximum tension in the thread will be 3mg.
- The sphere is raised to the height l (the length of the thread) and then released. At this point, the potential energy is at its maximum, and the kinetic energy is zero.
- The potential energy (PE) at the height l is given by:
PE=mgh=mgL
- Here, h=l is the height from which the sphere is released.
- As the sphere falls, the potential energy converts into kinetic energy (KE). At the lowest point, all the potential energy will have converted into kinetic energy.
- The kinetic energy at the lowest point is:
KE=12mv2
- By conservation of energy:
mgL=12mv2
- Rearranging the energy equation gives:
v2=2gL
- Thus, the velocity v at the lowest point is:
v=√2gL
- At the lowest point, the tension T in the thread must counteract both the weight of the sphere and provide the centripetal force required for circular motion.
- The weight of the sphere is mg.
- The centripetal force needed is given by:
Fc=mv2R
- Here, R=L (the radius of the circular path).
- Substituting v2:
Fc=m(2gL)L=2mg
- The total tension in the thread at the lowest point is:
T=mg+Fc=mg+2mg=3mg
- Therefore, the maximum tension in the thread when the sphere is at the lowest point is:
Tmax=3mg
The maximum tension in the thread will be 3mg.
Topper's Solved these Questions
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Taking it together
Explore 67 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Match the columns
Explore 3 Videos
- CIRCULAR MOTIONBook:DC PANDEYChapter:CIRCULAR MOTIONExercise:Integer
Explore 7 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBook:DC PANDEYChapter:CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONExercise:Level 2 Subjective
Explore 21 Videos
- COMMUNICATION SYSTEMBook:DC PANDEYChapter:COMMUNICATION SYSTEMExercise:Only One Option is Correct
Explore 27 Videos
Similar Questions
A small sphere of mass m suspended by a thread is first taken aside so that the thread forms the right angle with the vertical and then released. Find:
(a) the total acceleration of the sphere and the thread tension as a function of θ, the angle of deflection of the thread from the vertical,
(b) the thread tension at the moment when the vertical component of the sphere's velocity is maximum,
(c) the angle θ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally.
View SolutionAssume that the least load which would break a thread when simply suspended from it is M and that this load produces a strain of 1 percent at the moment of breaking. Also assume that Hooke's law applies to the thread right up to breakingpoint. A load of mass m is suspended from a thread of length λ. It is raised to a height and released. Find the least height to which the load must be raised so that it will will break the thread when allowed to fall.
View Solution
Knowledge Check
A small sphere of mass m suspended by a thread is first taken a side so that the thread forms the right angle with the vertical and then released, then
ATotal acceleration of sphere as a function of θ measured from the vertical is g√1+3cos3θBThread tension as a function of θ measured from the vertical is T=3mgcosθCThe angle θ between the thread and the vertical at the moment when the total acceleration vector of the sphere is directed horizontally is cos−11/√3.DThe thread tension at the moment when the vertical component of the sphere's velocity is maximum will be mg.An isolated charge q1 of mass m is suspended freely by a thread of length l. Another chaarges q2 is braought near it (r>>l). When q1 is in equilibrium tension in thread will be
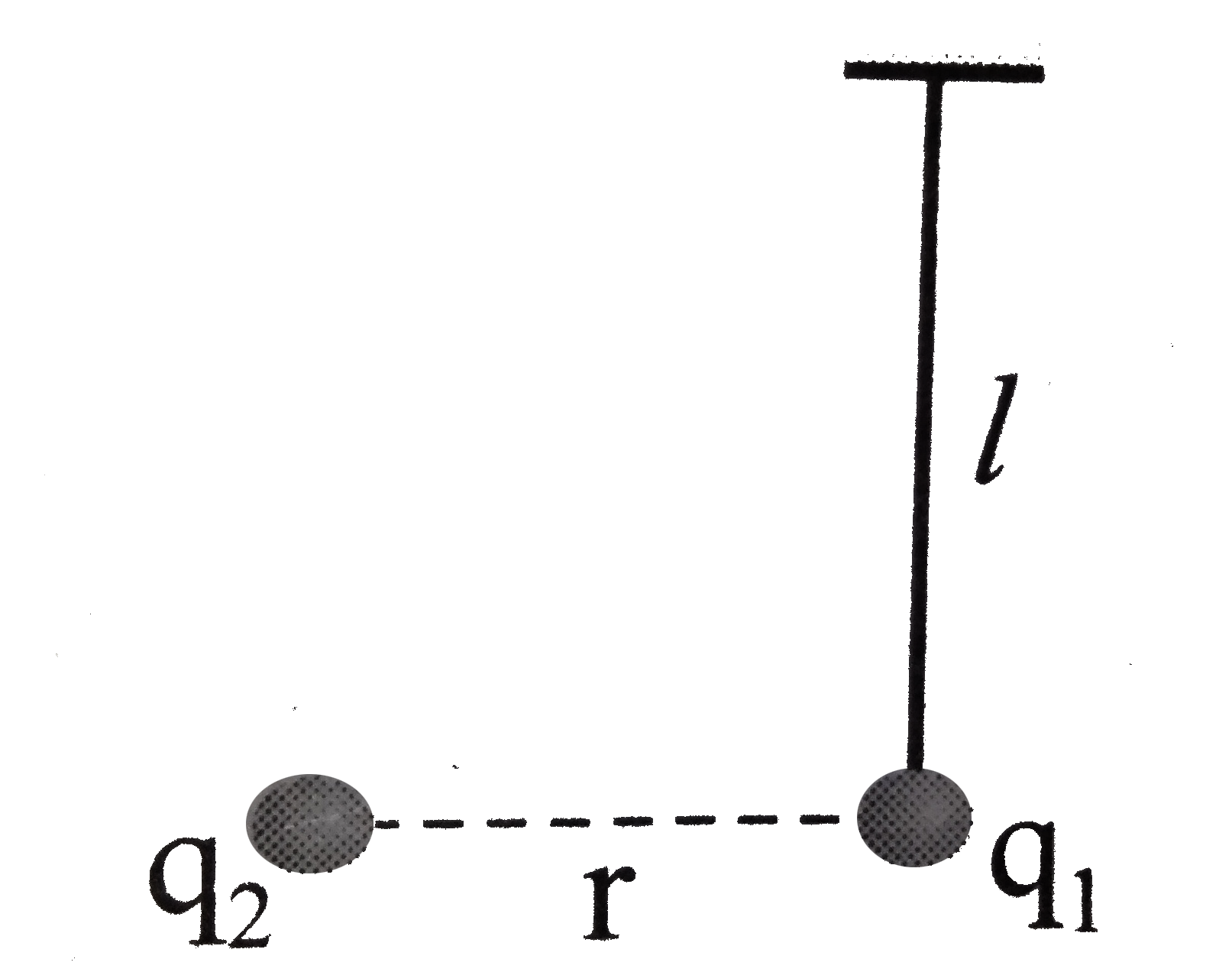 AmgB>mgC<mgDnone of these
AmgB>mgC<mgDnone of theseTwo small balls of mass m each are suspended side by side by two equal threds to length L. If the distance between the upper ends of the threads be a, the angle θ that the threads will make with the vertical due to attraction between the balls is :
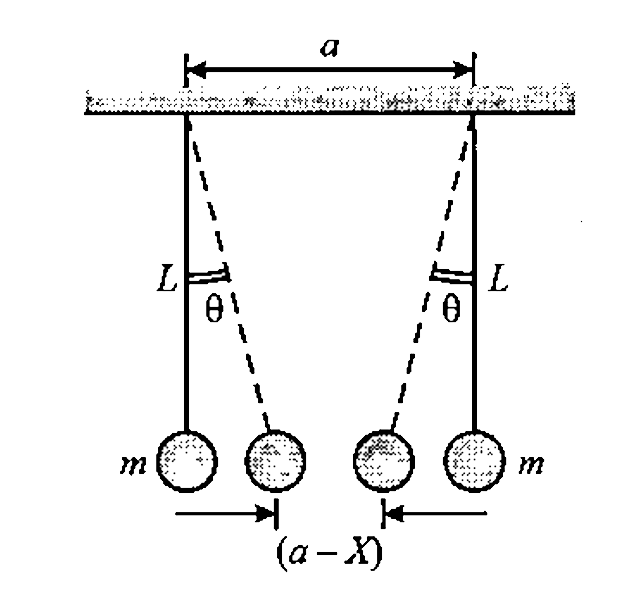 Atan−1(a−X)gmGBtan−1mG(a−X)2gCtan−1(a−X)2gmGDtan−1(a2−X2)gmG
Atan−1(a−X)gmGBtan−1mG(a−X)2gCtan−1(a−X)2gmGDtan−1(a2−X2)gmG
a small sphere of mass m susopended by a thread is first taken aside so that the thread forms the right angle with the verticle and then realease. (a) find the total acceleration of the sphere and the thread tension as a function of θ, the angle of deflection of the thread from the vertical. (b) Find the angle θ between the thread and the vertical. at the moment when the total acceleration vector of the sphere is directed (i) horizontally (ii)vertically upward and (iii) vertically downward.
View SolutionA ball of mass m is suspended by a thread of length l. With what minimum velocity has the point of suspension to be shifted in the horizontal direction for the ball to move along the circle about that point? What will be the tension of the thread at the moment it will be passing the horizontal position?
View SolutionA small cork ball A of mass m is suspended by a thread of length I. Another ball B is fixed at a distance I from point of suspension and distance l/2 from thread when is vertical, as shown in figure-1.444. Balls A and B have charges (+ q) each. Ball A is held by an external force such that the thread remains vertical.
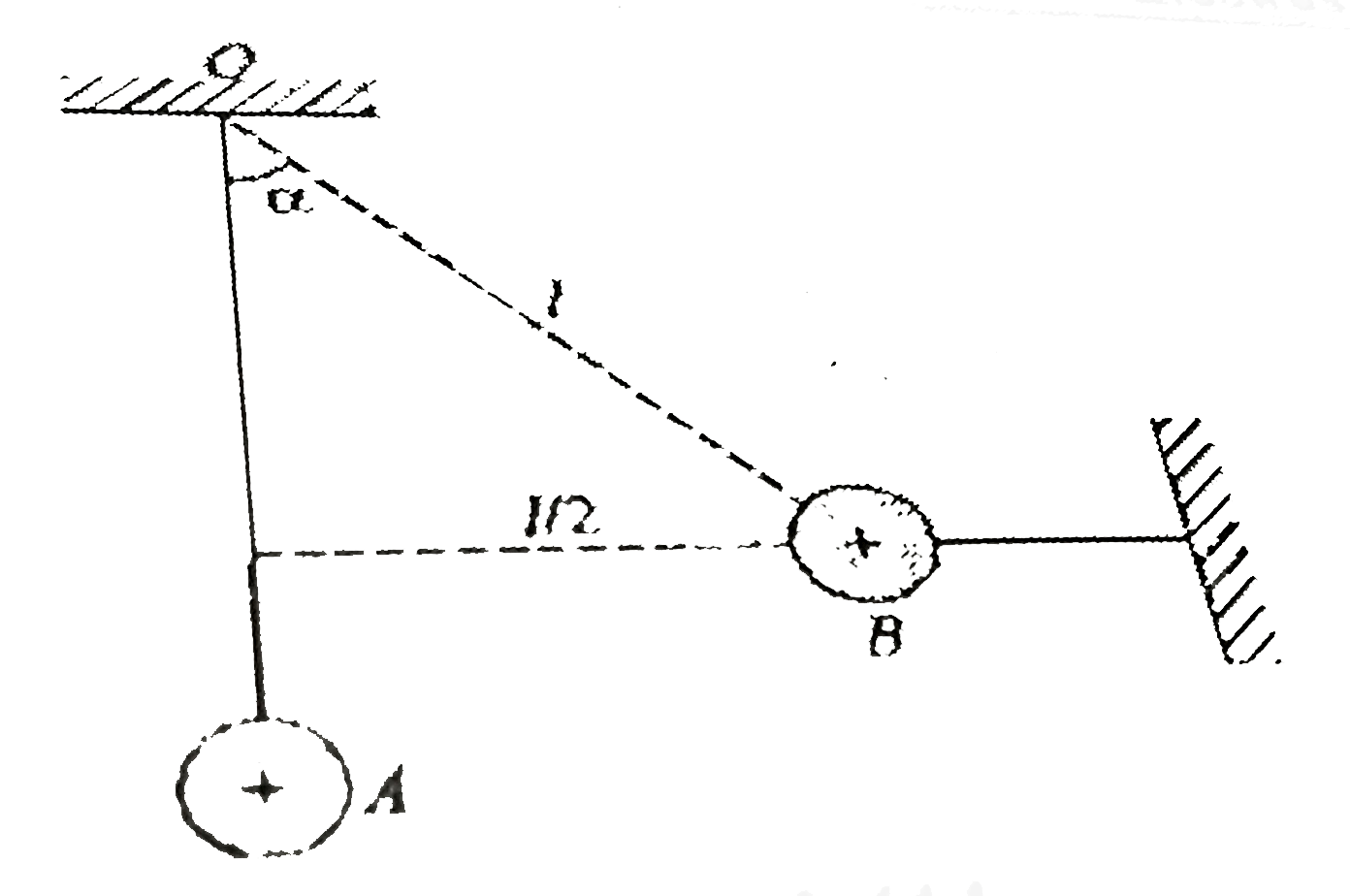
When ball A is released from rest, thread deflects through a . maximum angle of β=30∘, calculate m in terms of other parameters
View SolutionA simple pendulum consists of a small sphere of mass m suspended by a thread of length l. the sphere carries a positive charge q. The pendulum is placed in a uniform electric field of strength E directed vertically upwards. With what period will pendulum oscillate if the electrostatic force acting on the sphere is less than the gravitational force ?
View Solution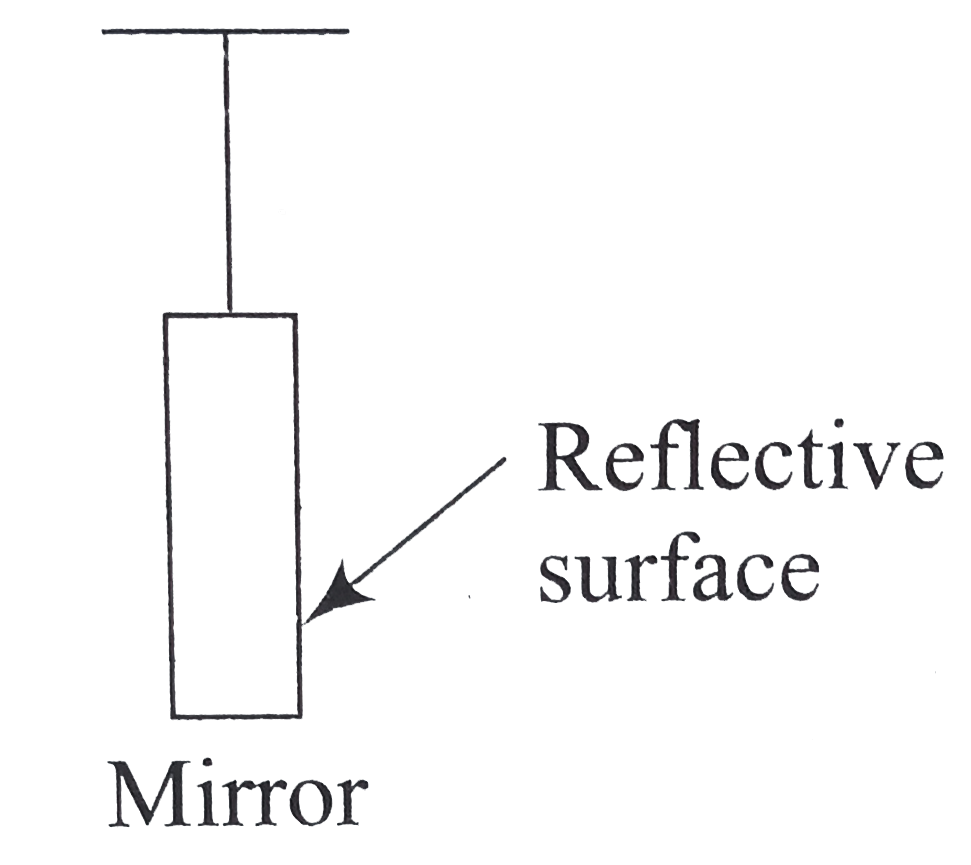
A small mirror of mass m is suspended by a light thread of length l. A short polse of laser falls on the mirror with energy E. Then, whoch of the following statement is correct?
View Solution

