IN a rotor, a hollow verticla cylindrical structure rotates about its axis and a person rests asgainst he inner wall. At a particular speed of the rotor, the floor below the person is removed and the person hangs resting against the wall without any floor. If the radius of the roter is 2m and the coefficient of static frictioin between the wall and theperson is 0.2, find the minimum speed at which the floor may be removed Take g=10ms2.
The situation is shown in figure below
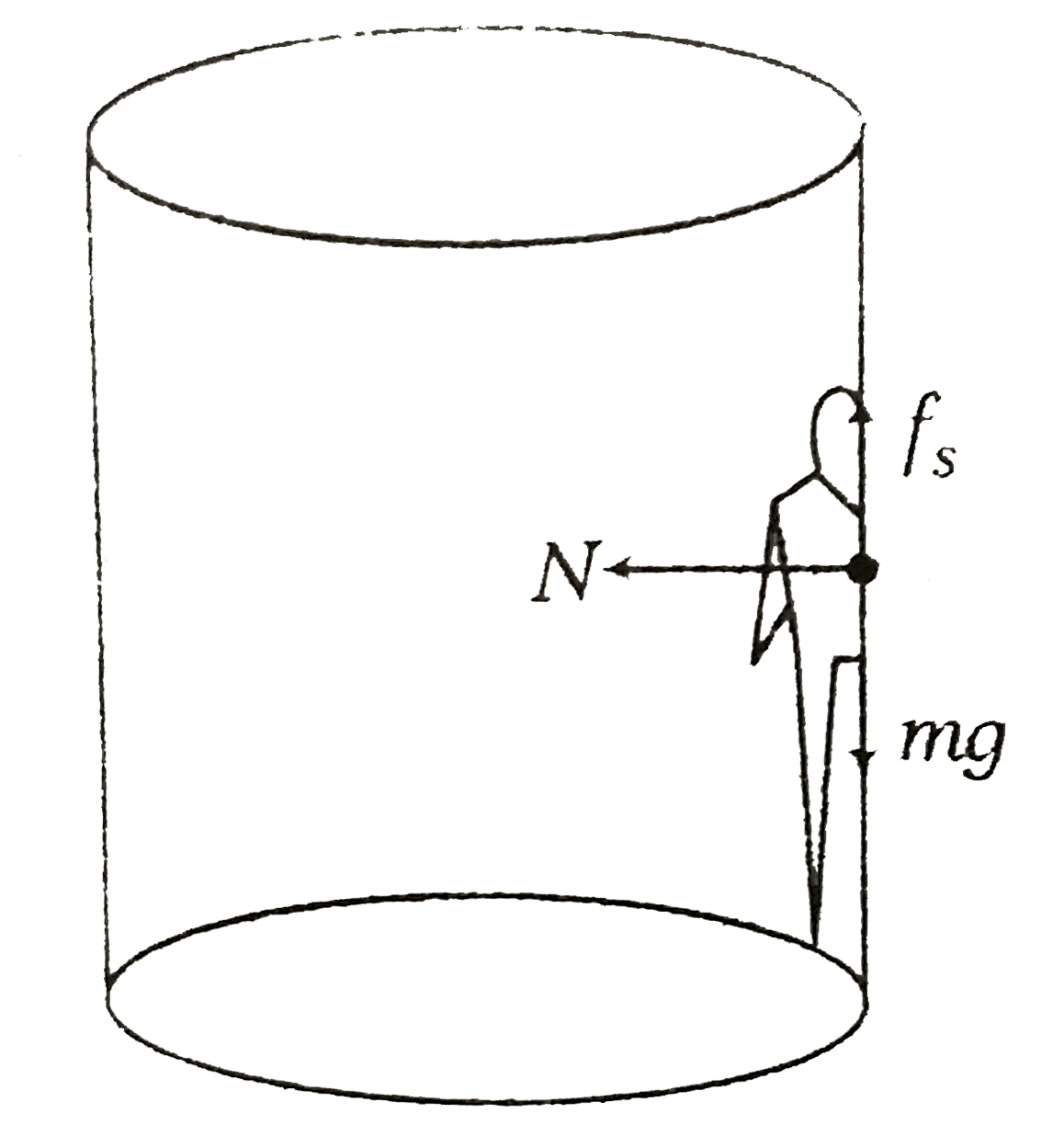
When the floor is removed, the forces on the person are
(i) weight mg downward.
(ii) normal force N due to the wall towards the centre.
(iii) frictional force fs parallel to the wall, upwards.
The person is moving in a circle with a uniform speed, so its acceleration is v2/r towards the centre.
For the minimum speed when the floor may be removed, the friction is limiting one and so equals μsN.
Theis gives
μsN=mg or μsmv2r=mg
or v=√rgμs=√2×100.2=10ms−1
Topper's Solved these Questions
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Solved Examples
2 Videos
- CIRCULAR MOTIONBOOK - DC PANDEYCHAPTER - CIRCULAR MOTIONEXERCISE - Miscellaneous Examples
5 Videos
- CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONBOOK - DC PANDEYCHAPTER - CENTRE OF MASS, LINEAR MOMENTUM AND COLLISIONEXERCISE - Level 2 Subjective
21 Videos
- COMMUNICATION SYSTEMBOOK - DC PANDEYCHAPTER - COMMUNICATION SYSTEMEXERCISE - Only One Option is Correct
27 Videos
Similar Questions
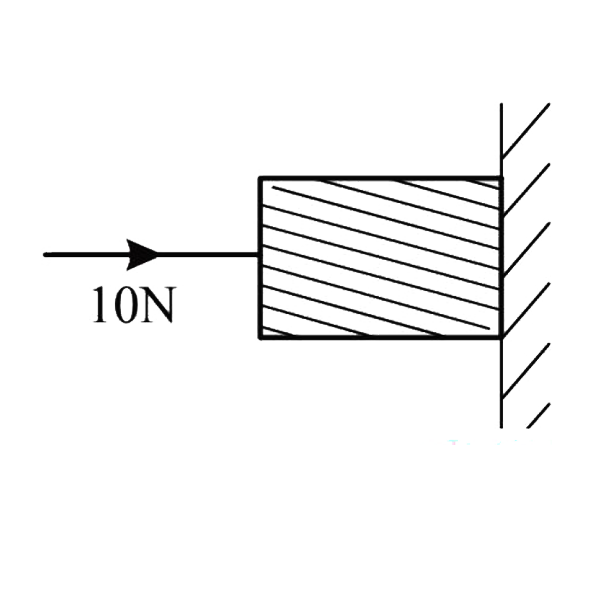
A horizontal force of 10N is necessary to just hold a block stationary against a wall.
The coefficient of fricition between the block and the wall is 0.2 then find the weight of the block. (g=10m/s2)

View SolutionA person stands in contact against the inner wall of a rotor of radius r. The coefficient of friction between the wall and the clothing is μ and the rotor is rotating about vertical axis. The minimum angular speed of the rotor so that the person does not slip downward is
View Solution
Knowledge Check
A person stands in contact against a wall of cylindrical drum of radius 'r' rotating with an angular velocity ω. If μ is coefficient ofn static fiction between the wall and the person , then the minimum rotational speed which enables the person to remain struck to the wall will be
A√gμrB√μrgC√2gμrD√grμIn a 'well of death' a ride drives round the inner wall of a hollow cylindrical chamber of siameter 20 m .If the coefficient of force friction between tyres and inner wall of a hollow cylinder is 0.5, then the minimum speed of the rider without sliding down will be
A7m/sB14m/sC2√7m/sD7√2m/sA motorcyclist rides in a horizontal circle along the inner wall of cylindrical chamber of radius r. If the coefficient of friction between the tyres and the wall of is μ, the minimum angular speed to prevent him from sidding down is
A√rμgB1r√μgC√grμD√rμg
A 90 kg man is standing in contact with the wall of a cylindrical drum of radius 2 m. The drum is rotating about its vertical axis with an angular speed of 100 rpm. Calculate the minimum rotational speed of the cylinder to enable the man to remain stuck to the wall when the floor is suddenly removed. The coefficient of friction between wall and clothing is 0.1.
View SolutionFind the minimum value of horizontal force (F) required on the block of mass m to keep it at rest on the wall. Given the coefficient of friction between the surfaces is μ.

View SolutionIn the diagram shown, friction is present only between therod and the wall. The mass of the rod is M and tht of the wedge is 3M. What is the minimum value of the coefficient of friction between the rod and the wall so that rod remains in the state of rest?
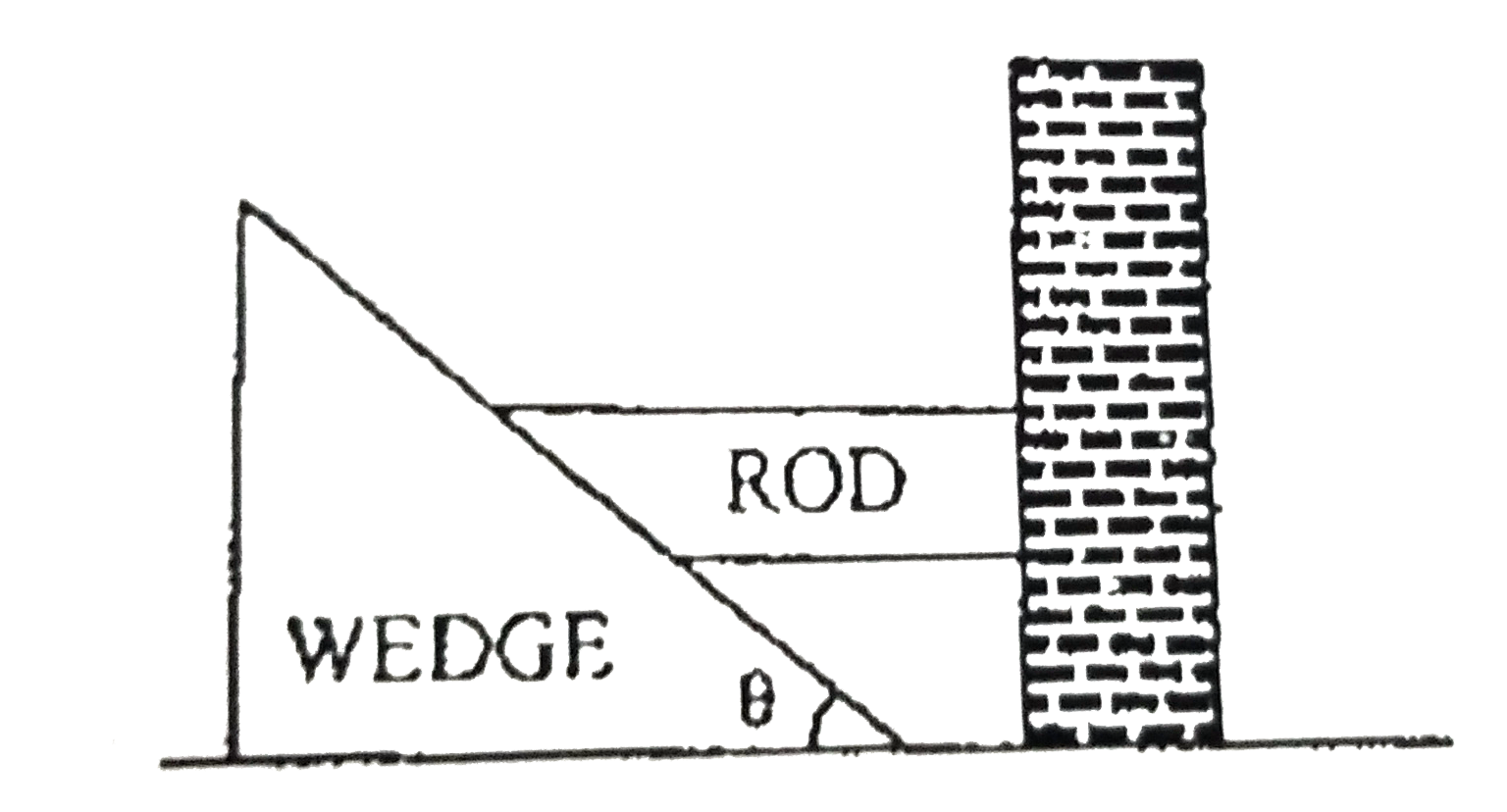
View SolutionA horizontal force of 10N is necessary to just hold a block stationary against as well. The coefficient of friction between the block and the wall is 0.2. The weight of the block is
View SolutionA person wants to drive on the vertical suirface of a large cylindrical wooden well commonly known as deathwell in a circus. The radius of the well 2 meter, and the coefficient of friction between the tyers of the motorcycle and the wall of the well is 0.2 the minimum speed the motorcyclist must have in order to prevent slipping should be
View Solution