Two balls are thrown simultaneously from ground with same velocity of $10 m s^{- 1}$ but different angles of projection with horizontally. Both balls fall at same distance $5 \sqrt{3} m$ from point of projection. What is the time interval between balls striking the ground ?

$(\sqrt{3} - 1) s$

$(\sqrt{3} + 1) s$

$\sqrt{3} s$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A

Updated on:21/07/2023

A ball is projected from the ground with speed u at an angle $α$ with horizontal. It collides with a wall at some distance from the point of projection and returns on the same level. Coefficient of restitution between the ball and the wall is e, then time taken in path AB and maximum height attained by the ball is

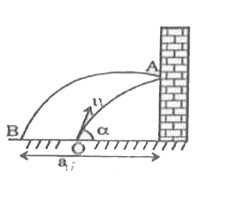A $\frac{a}{e u cos α}, \frac{u^{2} {sin}^{2} α}{2 g}$
B $\frac{a}{u cos α}, \frac{u^{2} {sin}^{2} α}{2 g}$
C $\frac{a}{e u cos α}, \frac{u^{2} {sin}^{2} α}{2 g}$
D $\frac{a}{u cos α}, \frac{u^{2} {sin}^{2} α}{2 g}$
A ball is thrown from the ground with a velocity of $20 \sqrt{3}$ m/s making an angle of $60^{\circ}$ with the horizontal. The ball will be at a height of 40 m from the ground after a time t equal to $(g = 10 m s^{- 2})$
A $\sqrt{2}$ sec
B $\sqrt{3}$ sec
C2 sec
D3 sec
A ball is thrown straight upward with a speed v from a point h meter above the ground. The time taken for the ball to strike the ground is
A $\frac{v}{g} [1 + \sqrt{1 + \frac{2 h g}{v^{2}}}]$
B $\frac{v}{g} [1 - \sqrt{1 - \frac{2 h g}{v^{2}}}]$
C $\frac{v}{g} [1 - \sqrt{1 + \frac{2 h g}{v^{2}}}]$
D $\frac{v}{g} [2 + \frac{2 h g}{v^{2}}]$