Derive an expression for potenstial energy of bar magnet in a uniform magnetic field.
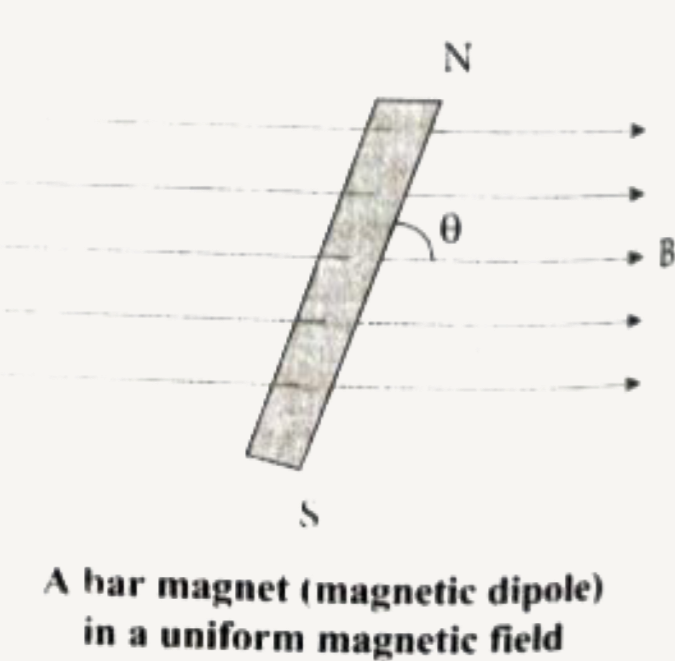
Derive an expression for potenstial energy of bar magnet in a uniform magnetic field.Solution in Tamil

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

When a bar magnet ( magnetic dipole) of dipole moment p → m is held at an angle θ with the direction of a uniform magnetic field B → , as shown in Figure the magnitude of the torque acting on the dipole is
ocr_image
| τ → B | = | p → m | | B → | sin θ
If the dipole is rotated through a very small angular displacement d θ against the torque τ B at constant angular velocity, then the work done by external torque ( τ → ext ) for this small angular displacement is given by
d W = | τ → axt | d θ
Since the bar magnet to be moved at constant angular velocity , it implies | τ → B | = | τ → ext |
d W = p m B sin θ d θ
Total work done in rotaiting the dipole from θ ′ to θ is
W = ∫ θ θ τ d θ = ∫ θ θ p m B sin θ d θ = p m B [ - cos θ d θ ] θ θ ,
W = p m B ( cos θ - cos θ ′ )
This work done is stored as potential energy in bar magnet at an angle θ when it is rotated from θ ′ to θ and it can be written as
U = p m B ( cos θ - cos θ ′ ) ....(1)
In fact, the equation (1) gives the difference in potential energy between the angular position θ ′ and θ . We can choose the reference point θ ′ = 90 ∘ , so that second term in the equation becomes zero and the equation (1) can be written as
U = - p m B ( cos θ ) ....(2)
The potential energy stored in a bar magnet in a uniform magnetic field is given by
U = - p → m ⋅ B → .......(3)
Case 1
(i) If θ = 0 ∘ , then
U = p m B ( cos 0 ∘ ) = - p m B
(ii) If θ = 180 ∘ , then
U = p m B ( cos 180 ∘ ) = p m B
We can infer from the above two results , the potential energy of the bar magnet is minimum when it is aligned along the external magnetic field and maximum when the bar magnet is aligned anti - parallel to external magnetic field.

Updated on:21/07/2023
|