Question

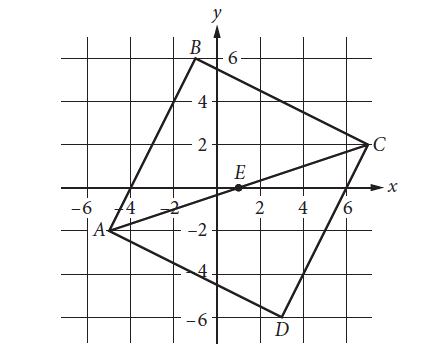
In the xy-plane above, ABCD is a square and point E is the center of the square. The coordinates of points C and E are (7, 2) and (1, 0), respectively. Which of the following is an equation of the line that passes through points B and D ?

Options

A. `y= −3x−1`
B. `y= −3(x−1)`
C. `y= -(1)/(3)x+4`
D. `y= -(1)/(3)x-1`

Explanation

Choice B is correct. In the xy-plane, the slope m of the line that passes through the points `(x_(1), y_(1)) and (x_(2), y_(2))` is `m =(y_(2)-y_(1))/(x_(2)-x_(1))`. Thus, the slope of the line through the points C(7, 2) and E(1, 0) is `(2-0)/(7-1)` , which simplifies to `(2)/(6)=(1)/(3)` . Therefore, diagonal AC has a slope of `(1)/(3)` . The other diagonal of the square is a segment of the line that passes through points B and D. The diagonals of a square are perpendicular, and so the product of the slopes of the diagonals is equal to −1. Thus, the slope of the line that passes through B and D is −3 because `(1)/(3) (−3) = −1`. Hence, an equation of the line that passes through B and D can be written as y = −3x + b, where b is the y-intercept of the line. Since diagonal BD will pass through the center of the square, E(1, 0), the equation 0 = −3(1) + b holds. Solving this equation for b gives b = 3. Therefore, an equation of the line that passes through points B and D is y = −3x + 3, which can be rewritten as y = −3(x − 1).
Choices A, C, and D are incorrect and may result from a conceptual error or a calculation error.