What is the sum of all values of m that satisfy 2m2−16m+8=0 ?
-8
−4√3
4√3
8
Choice D is correct. The problem asks for the sum of the roots of the quadratic equation 2m2−16m+8=0. Dividing each side of the equation by 2 gives m2−8m+4=0. If the roots of m2−8m+4=0 are s1ands2, then the equation can be factored as m2−8m+4=(m−s1)(m−s2)=0. Looking at the coefficient of x on each side of m2−8m+4=(m−s1)(m−s2) gives −8=−s1−s2,ors1+s2=8.
Alternatively, one can apply the quadratic formula to either 2m2−16m+8=0 or m2−8m+4=0. The quadratic formula gives two solutions, 4−2√3 and 4+2√3 whose sum is 8.
Choices A, B, and C are incorrect and may result from calculation errors when applying the quadratic formula or a sign error when determining the sum of the roots of a quadratic equation from its coefficients.
Similar Questions
Knowledge Check
The product of all the solutions to the equation 3y2+4v−2=0 is M. What is the value of M ?
A−3B−23C−13D43
The real value of a for which the value of m satisfying the equation (a2−1)m2−(2a−3)m+a=0 given the slope of a line parallel to the y-axis is(a) 32 (b) 0 (c) 1 (d) ±1
View SolutionFor what value of m is x3−2mx2+16 Divisible by x+2 ?
View SolutionFind all values of 'm' which (2m−3)x2+2mx+4<0 for all real x.
View SolutionFind the sum of the possible integer values of m:
2m+n=10
m(n−1)=9
View SolutionThe real value of a for which the valye of m satisfying the equation (a2−1)m2−(2a−3)m+a=0 gives the slope of a line parallel to the y-axis is
View SolutionLet S be the sum of all possible determinants of order 2 having 0,1,2 and 3 as their elements,. Find the common root α of the equations x2+ax+[m+1]=0,
x2+bx+[m+4]=0
and x2−cx+[m+15]=0
such that α>Swherea+b+c=0 and
m=∑n→001n2n∑r=1r√n2+r2
and [.] denotes the greates integer function.
View SolutionFour paticle of masses m1=2m,m2=4m,m3=mandm4 are placed at four corners of a square. What should be the value of m4 so that the centres of mass of all the four particle are exactly at the centre of the square ?
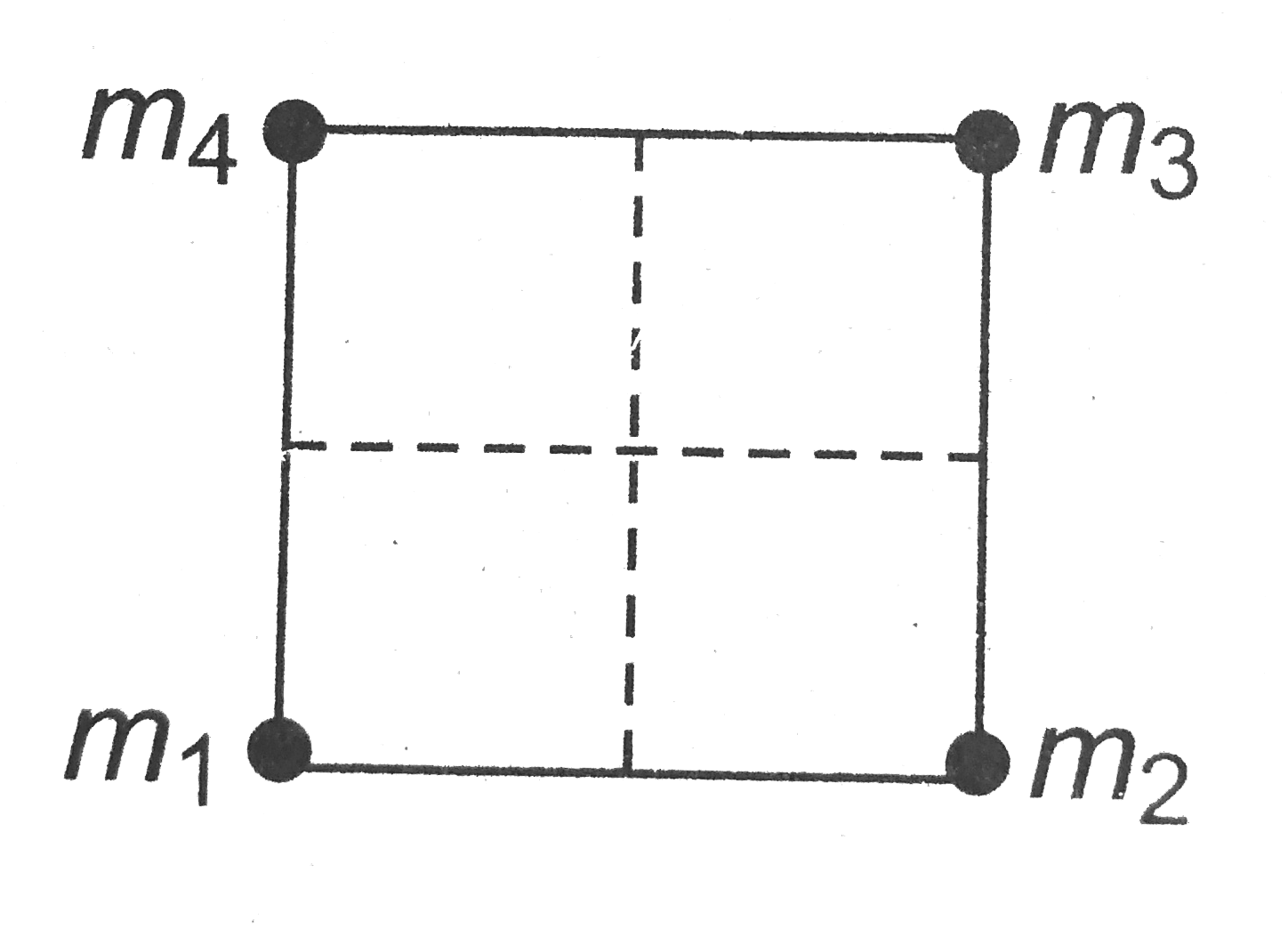
View Solution
