Which of the following equations has a graph in the xy-plane for which y is always greater than or equal to −1 ?
y=|x|−2
y=x2−2
y=(x−2)2
y=x3−2
To determine which equation has a graph in the xy-plane for which y is always greater than or equal to -1, we will analyze each option provided in the question.
Let's denote the options as follows:
1. Option A: y=|x|−2
2. Option B: y=x2−2
3. Option C: y=(x−2)2
4. Option D: y=x2+1
Step 1: Analyze each option
Option A: y=|x|−2
The minimum value of |x| is 0 (when x=0).
Thus, the minimum value of y is:
y=0−2=−2
This means y can be less than -1. Therefore, this option does not satisfy the condition.
Option B: y=x2−2
The minimum value of x2 is 0 (when x=0).
Thus, the minimum value of y is:
y=0−2=−2
This means y can also be less than -1. Therefore, this option does not satisfy the condition.
Option C: y=(x−2)2
The minimum value of (x−2)2 is 0 (when x=2).
Thus, the minimum value of y is:
y=0
Since 0 is greater than -1, this option satisfies the condition.
Option D: y=x2+1
The minimum value of x2 is 0 (when x=0).
Thus, the minimum value of y is:
y=0+1=1
Since 1 is greater than -1, this option also satisfies the condition.
Step 2: Conclusion
From the analysis, we find that both Option C and Option D satisfy the condition of y being greater than or equal to -1. However, since the question asks for which equation has a graph where y is always greater than or equal to -1, Option C is the only one that meets the criteria of being equal to 0 at its minimum.
Thus, the correct answer is:
Option C: y=(x−2)2
1. Option A: y=|x|−2
2. Option B: y=x2−2
3. Option C: y=(x−2)2
4. Option D: y=x2+1
The minimum value of |x| is 0 (when x=0).
Thus, the minimum value of y is:
y=0−2=−2
This means y can be less than -1. Therefore, this option does not satisfy the condition.
The minimum value of x2 is 0 (when x=0).
Thus, the minimum value of y is:
y=0−2=−2
This means y can also be less than -1. Therefore, this option does not satisfy the condition.
The minimum value of (x−2)2 is 0 (when x=2).
Thus, the minimum value of y is:
y=0
Since 0 is greater than -1, this option satisfies the condition.
The minimum value of x2 is 0 (when x=0).
Thus, the minimum value of y is:
y=0+1=1
Since 1 is greater than -1, this option also satisfies the condition.
From the analysis, we find that both Option C and Option D satisfy the condition of y being greater than or equal to -1. However, since the question asks for which equation has a graph where y is always greater than or equal to -1, Option C is the only one that meets the criteria of being equal to 0 at its minimum.
Option C: y=(x−2)2
Similar Questions
Knowledge Check
Which of the following equations has a graph for which all roots are greater than 0 ?
Ay=4|x|By=x2−4Cy=(x−2)2Dy=x(x−2)2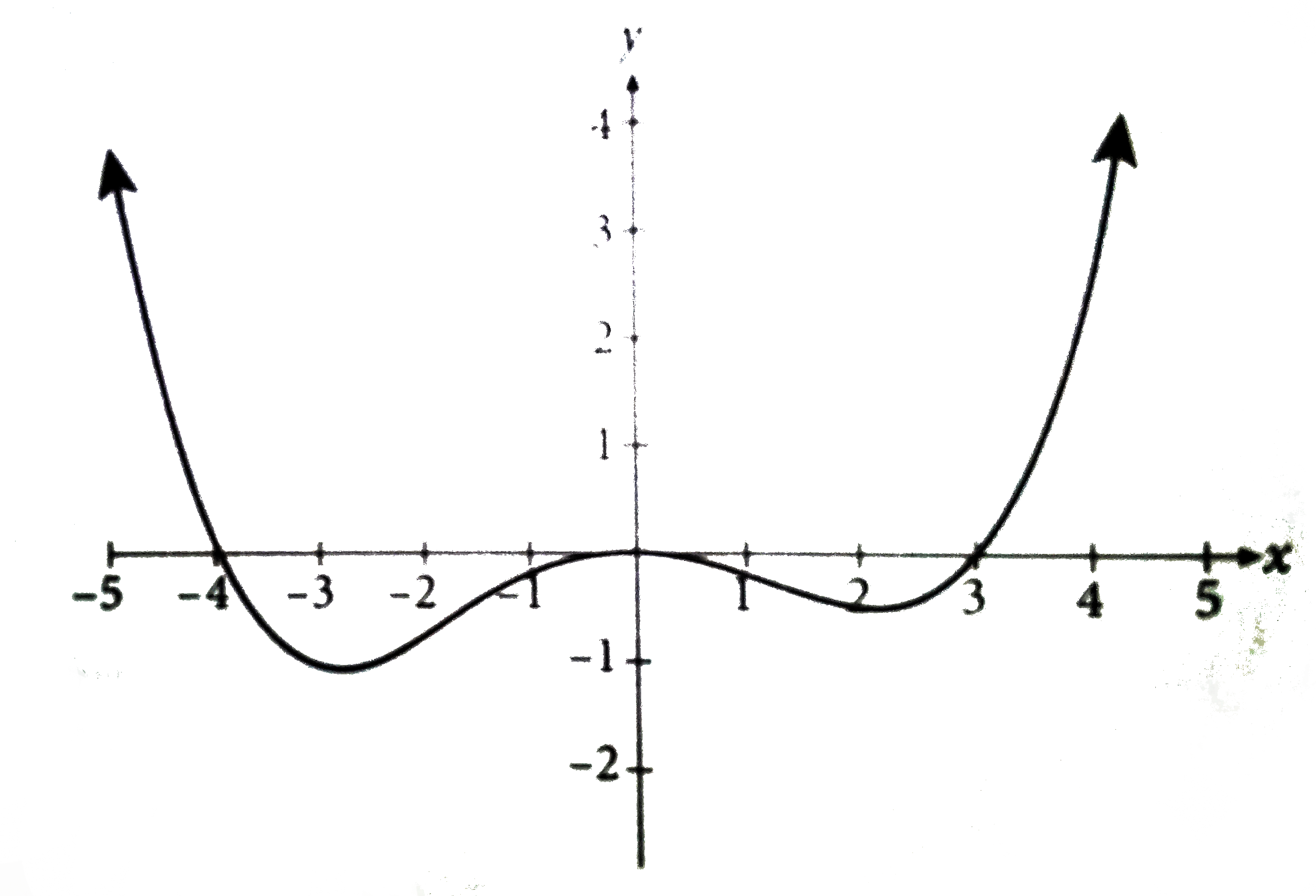
Which of the following could be the equation of the graph in the xy-plane shown above?Af(x)=x(x+3)(x−4)Bf(x)=x(x+4)(x−3)Cf(x)=x2(x+3)(x−4)Df(x)=x2(x+4)(x−3)Which of the following fractions are greater than 12?
A712−112B317+717C717−317D58−28
Which of the following has greater bond length ? .
View SolutionWhich of the following compounds has the greater dipole moment?
_E01_274_Q01.png)
View SolutionWhich of the following has ΔS∘ greater than zero
View SolutionWhich of the following MOs has more than one nodal plane?
View SolutionIn which of the following case pH is greater than 7 ?
View Solution