The capacitance of a parallel plate capacitor is 50 pF and the distance between the plates is 4mm. It is charged to 200 V and then the charging battery is removed. Now a dielectric slab (κ=4) of thickness 2mm is placed. Determine (i) final charge on each plate (ii) finial potential difference between the plates (iii) final energy is the capacitor.
To solve the problem step by step, we will follow the given information and apply the relevant formulas for capacitors.
Given Data:
- Capacitance of the capacitor, C=50pF=50×10−12F
- Distance between the plates, D=4mm=4×10−3m
- Voltage, V=200V
- Dielectric constant, κ=4
- Thickness of the dielectric slab, t=2mm=2×10−3m
Step 1: Calculate the Initial Charge on the Capacitor
The charge Q on the capacitor can be calculated using the formula:
Q=C×V
Substituting the values:
Q=50×10−12F×200V=10×10−9C=10nC
Step 2: Calculate the New Capacitance with the Dielectric
When a dielectric slab is inserted, the new capacitance C′ can be calculated using the formula:
C′=Aϵ0D′
Where D′ is the new effective distance between the plates. The effective distance can be calculated as:
D′=(D−t)+tκ=(4mm−2mm)+2mm4=2mm+0.5mm=2.5mm=2.5×10−3m
Now substituting into the capacitance formula, we have:
C′=C⋅κD−tD=50×10−12⋅42.5×10−3=80×10−12F=80pF
Step 3: Calculate the Final Potential Difference
The potential difference V′ after inserting the dielectric can be calculated using:
V′=QC′
Substituting the values:
V′=10×10−9C80×10−12F=125V
Step 4: Calculate the Final Energy in the Capacitor
The energy U′ stored in the capacitor can be calculated using the formula:
U′=12C′(V′)2
Substituting the values:
U′=12×80×10−12×(125)2
Calculating:
U′=12×80×10−12×15625=625×10−9J=6.25×10−7J
Final Answers:
1. Final charge on each plate: Q=10nC
2. Final potential difference between the plates: V′=125V
3. Final energy in the capacitor: U′=6.25×10−7J
- Capacitance of the capacitor, C=50pF=50×10−12F
- Distance between the plates, D=4mm=4×10−3m
- Voltage, V=200V
- Dielectric constant, κ=4
- Thickness of the dielectric slab, t=2mm=2×10−3m
The charge Q on the capacitor can be calculated using the formula:
Q=C×V
Substituting the values:
Q=50×10−12F×200V=10×10−9C=10nC
When a dielectric slab is inserted, the new capacitance C′ can be calculated using the formula:
C′=Aϵ0D′
Where D′ is the new effective distance between the plates. The effective distance can be calculated as:
D′=(D−t)+tκ=(4mm−2mm)+2mm4=2mm+0.5mm=2.5mm=2.5×10−3m
Now substituting into the capacitance formula, we have:
C′=C⋅κD−tD=50×10−12⋅42.5×10−3=80×10−12F=80pF
The potential difference V′ after inserting the dielectric can be calculated using:
V′=QC′
Substituting the values:
V′=10×10−9C80×10−12F=125V
The energy U′ stored in the capacitor can be calculated using the formula:
U′=12C′(V′)2
Substituting the values:
U′=12×80×10−12×(125)2
Calculating:
U′=12×80×10−12×15625=625×10−9J=6.25×10−7J
1. Final charge on each plate: Q=10nC
2. Final potential difference between the plates: V′=125V
3. Final energy in the capacitor: U′=6.25×10−7J
Topper's Solved these Questions
- CAPACITORSBook:SL ARORAChapter:CAPACITORSExercise:Problem From Competitive Examinations
Explore 17 Videos
- CAPACITORSBook:SL ARORAChapter:CAPACITORSExercise:problem for self practive
Explore 65 Videos
- ATOMS, NUCLEI AND MOLECULESBook:SL ARORAChapter:ATOMS, NUCLEI AND MOLECULESExercise:Problems For Self Practice
Explore 87 Videos
- CHEMICAL EFFECT OF CURRENTBook:SL ARORAChapter:CHEMICAL EFFECT OF CURRENTExercise:TYPE-B
Explore 5 Videos
Similar Questions
A parallel plate capacitor (C=50μF.d=4mm) is charged to 200V and then charging battery is removed. Now a dielectric slab (K=4) of thickness 2mm is placed between the plates. Find new potential difference across capacitor.
View SolutionA parallel plate capacitor having plate area A and separation between the plates d is charged to potential V.The energy stored in capacitor is ....???
View Solution
Knowledge Check
After charging a capacitor the battery is removed. Now by placing a dielectric slab between the plates
Athe potential difference between the plates and the energy stored will decreases but the charge on plates will remains sameBthe charge on the plates will decreases and the potential difference between the plates will increasesCthe potential difference between the plates will increases and energy stored will decreases but the charge on the plates will remains sameDthe potential difference, energy stored and the charge will remain unchangedSeparation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-
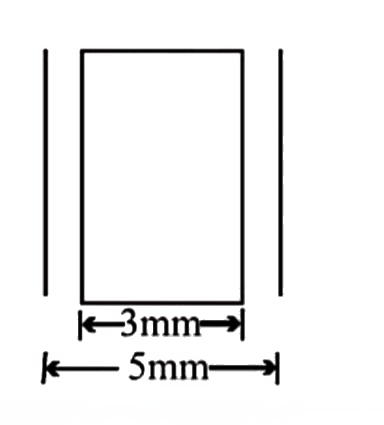 A18.5VB13.5VC11.5VD6.5V
A18.5VB13.5VC11.5VD6.5VA parallel plate copacitor is first charged and then isolated, and a dielelctric slab is introduced between the plates. The quantity that remains unchanged is.
ACharge QBPotential VCCapacity CDEnergy U
A parallel plate capacitor is charged by a battery . After sometime the battery is disconnected and a dielectric slab with its thickness equal to the plate separation is inserted between the plates . How will potential difference between the plates ? Justify your answer
View SolutionEach plate of a parallel plate capacitor has a charge q on it. The capacitor is now connected to a battery. Now,
View SolutionA parallel plate capacitor is charged completely and then disconnected from the battery. IF the separation between the plates is reduced by 50% and the space between the plates if filled with a dielectric slab of dielectric constant 10, then the potential difference between the plates
View SolutionA parallel plate capacitor has smooth square plates of side ''a''. It is charged by a battery so that, the charge density becomes σ. After charging, the battery is disconnected. Now a smooth dielectric slab of length a which can fill the space between the plates is introduced between the plates from one side between the plates.
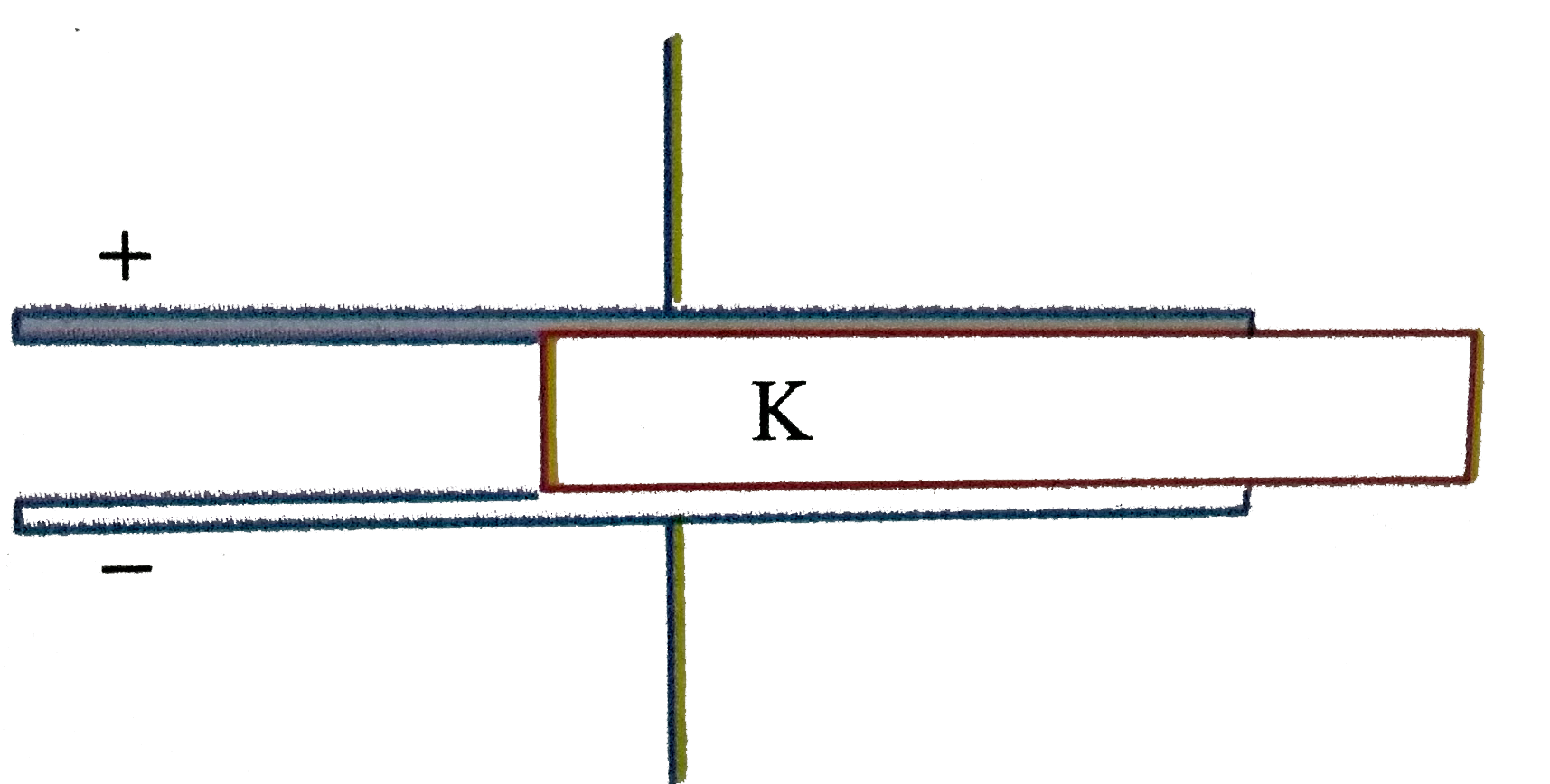 .
.
View SolutionThe space between plates of a parallel plate capacitor is filled by a dielectric and it is charged and then battery is removed. Now dielectric slab is slowly drawn out of the capacitor parallel to the plates. The variatiton of the potential of capacitor with respect to the length of the dielectric plate drawn out is
View Solution

